Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 9

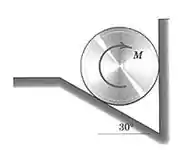
6/9) O cilindro homogêneo de 30   k g com 400   m m de diâmeto , está em repouso apoiado contra as superfícies vertical e inclinada , como mostrado . Se o coeficiente de atrito estático entre o cilindro e as superfícies vale 0,30 , calcule o momento M aplicado no sentido horário que faria o cilindro deslizar .

Passo 1

Falaaaai meus amores, show de bola?

Bora pra mais um?

Vamos começar com o nosso D.C.L, show?

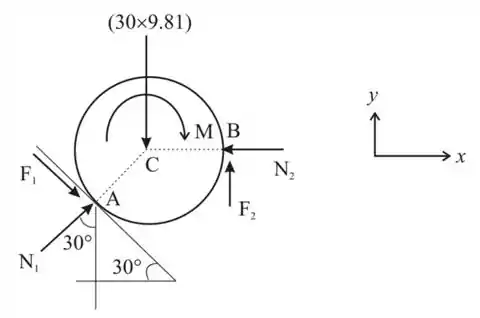
Passo 2

Bom pelo enunciado, retirando toda a perfumaria, temos que a massa do cilindro é de 30 k g , e o diâmetro é de   400   m m , o coeficiente de atrito estático entre o cilindro e as superfícies é μ s = 0.30 .

Para deslizamento iminente, em ambas as superfícies temos

F 1 = μ s N 1

F 1 = 0.3 N 1

F 2 = μ s N 2

F 2 = 0.3 N 2

Passo 3

Vamos escrever a equação de equilíbrio

∑ F x = 0

F 1 cos ⁡ 30 + N 1 sin ⁡ 30 - N 2 = 0                   ( 1 )

∑ F y = 0

F 2 + N 1 cos ⁡ 30 - 30 × 9.81 - F 1 sin ⁡ 30 = 0                   ( 2 )

Passo 4

Da expressão (1)

0.3 N 1 cos ⁡ 30 + N 1 sin ⁡ 30 - N 2 = 0

0.7598 N 1 - N 2 = 0

N 2 = 0.7598 N 1                   ( 3 )

Passo 5

Da expressão (2)

0.3 N 2 + N 1 cos ⁡ 30 - 294.3 - 0.30 N 1 sin ⁡ 30 = 0

0.3 N 2 + 0.716 N 1 - 294.3 = 0

0.3 0.7598 N 1 + 0.716 N 1 = 294.3

N 1 = 311.78   N

Da expressão (3)

N 2 = 0.7598 N 1

N 2 = 236.89   N

F 1 = 0.3 N 1

F 1 = 0.3 × 311.78   N

F 1 = 93.534   N

F 2 = 0.3 N 2

F 2 = 0.3 × 236.89   N

F 2 = 71.067   N

Passo 6

Tomemos momento sobre o ponto C

M - F 2 × 200 - F 1 × 200 = 0

M - 71.067 × 200 - 93.534 × 200 = 0

M = 32920.2   N ⋅ m m

M = 32.92   N ⋅ m

Resposta

N B = 311.78   N N A = 236.89   N M = 32.92   N . m

De boa galera? Então bora resolver mais exercícios como esse!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/14) O homem pesando 80k g , com centro de gravidade G , suporta o tambor de 34k g , como mostrado . Ache a maior distância x na qual o homem pode se posicionar sem escorregar , se o coeficiente de a
6/7) Dois homens estão deslizando um caixote de 100k g paracima no plano inclinado . Se o homem de baixo empurra horizontalmente com uma força de 500N e se o coeficiente de atrito dinâmico vale 0,40 ,
6/12) A roda de 50k g rola sobre seu eixo subindo a rampa circular sob a ação do cilindro de 12k g preso a um cabo enrolado a sua volta . Determine o ângulo θ para o qual a roda chega ao repouso , ass
6/10) Calcule a força P necessária para iniciar o movimento do bloco de 24k g para cima no plano inclinado de 10 ° . O coeficiente de atrito estático para cada par de superfícies vale 0,30 .
6/1) A força P é aplicada ao caixote de 90k g , que está em repouso antes que ela seja aplicada . Determine o módulo e a direção da força de atrito F exercida pela superfície horizontal sobre o caixot