104. Um pequeno compressor de ar para a cabine de um avião é composto pela turbina de , que aciona o soprador de a uma velocidade de . O eixo do conjunto está montado transversalmente a direção de vôo e é visualizado a partir da traseira da aeronave. Os raios de giração de e de são e , respectivamente. Calcule as forças radiais exercidas sobre o eixo pelos mancais em e , se a aeronave executa um rolamento no sentido horário (rotação em torno do eixo longitudinal de vôo) de visto da parte traseira da aeronave. Despreze os pequenos momentos provocados pelos pesos dos rotores. Desenhe um diagrama de corpo livre do eixo quando visto de cima e indique a forma da deflexão de sua linha de centro.
Passo 1
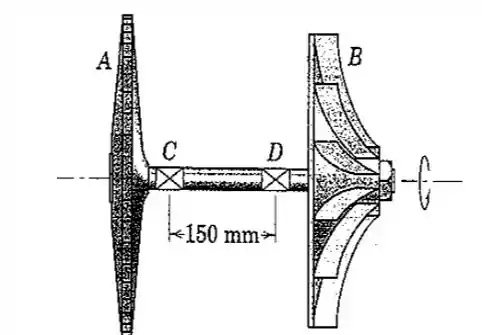
Primeiramente vamos fazer a representação esquemáticas das forças e momentos que estão agindo no nosso compressor, para isso tomando uma vista que seja mais apropriada para análise.

Passo 2
Bom! Agora vamos definir o quanto vale o nosso giro . Olho lá, que a questão nos forneceu a velocidade em . Para converter para , basta dividir tudo por e encontramos o que queremos:
Como já temos o valor da precessão, que é igual a , bora tratar de determinar o momento de inércia do noss sistema, que é composto pela turbina e o soprador . Para isso, basta multiplicar a massa de cada um pelo seu respectivo raio de giração ao quadrado:
Obtido, o momento de inércia , a velocidade de giro e o valor da precessão , bora tratar de obter o momento através da fórmula que todo mundo já tá careca de saber:
E aí que vem a grande mágica da questão, porque esse momento que acabamos de obter, na verdade é o momento oriundo da atuação das forças e , um binário de forças com uma distância de da linha de atuação de uma força pra outra. Logo, obtemos que:
Passo 3
E aqui está o diagrama de corpo livre do eixo quando visto de cima com a respectiva forma da deflexão de sua linha de centro.
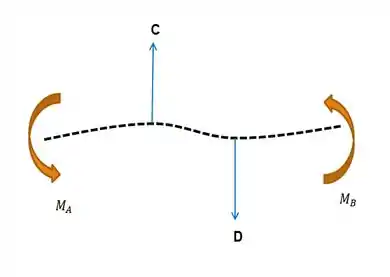
Resposta
