Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 22
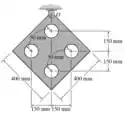
Determine o momento de inércia da massa da placa fina em relação a um eixo perpendicular à página e passando pelo ponto . O material tem uma massa por unidade de área de 20 kg/m2.
Passo 1
A placa pode ser subdivida em duas partes, sendo elas: a placa quadrada e os quatro círculos. Podemos calcular as massas de cada uma dessas partes, com isso,
e
Vale a pena lembrar que a massa que encontramos é de apenas um círculo, mas temos 4 círculos na geometria do problema. Essa informação nós iremos utilizar no passo seguinte.
Passo 2
A partir do cálculo das massas, podemos calcular o momento de inércia passando pelo ponto . Então,
Passo 3
O momento de inércia de massa que o enunciado pede pode ser calculado pelo teorema dos eixos paralelos, , onde e . Então,
Resposta
Exercícios de Livros Relacionados
Determine a aceleração angular α → para o disco circular que rola do Prob. 7/135. Utilize os resultados fornecidos na resposta para aquele problema.
Determine a velocidade v → do ponto A sobre o disco do Prob. 7/135 para a posição mostrada.
O disco circular de raio r está montado no eixo, que é articulado em O de modo que possa girar em torno do eixo vertical z 0 . Se o disco rola com velocidade constante sem deslizar e realiza uma volta
Resolva o Prob. 7/140 quando β , em vez de ser constante em 20°, está crescendo à taxa constante de 120r p m . Encontre a quantidade de movimento angular H O → do disco para o instante β = 20 ° . Calc
O disco circular uniforme com 100m m de raio e pequena espessura possui massa de 3.6kg e está girando em torno de seu eixo y’ à taxa N = 300r p m com seu plano de rotação inclinado em um ângulo consta