Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 15
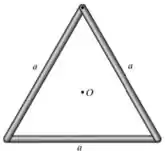
Cada uma das três barras finas tem uma massa . Determine o momento de inércia da montagem em relação a um eixo que é perpendicular à página e passa pelo ponto central .
Passo 1
Esse problema é para que você treine a sua visão geométrica e para que você trabalhe com trigonometria. Primeiro, temos que encontrar a distância do ponto até o centro de cada barra. Por geometria plana no triângulo retângulo, essa distância será igual a . Então,
Resposta
Exercícios de Livros Relacionados
O centro O da nave espacial está se deslocando através do espaço com uma velocidade constante. Durante o período do movimento anterior à estabilização, a nave espacial possui uma taxa de rotação const
O disco circular com 100 mm de raio gira em torno de seu eixo z com a velocidade constante p = 240r p m , e o braço O C B gira em torno do eixo Y na velocidade constante N = 30r p m . Determine a velo
Para as condições descritas no Exemplo 7/2, exceto que γ está aumentando na taxa constante de 3 ⋅ πr a d / s , determine a velocidade angular ω e a aceleração angular α do rotor quando a posição γ = 3
O disco possui uma velocidade angular constante p em torno de seu eixo z , e o garfo A possui uma velocidade angular constante ω 2 em torno de seu eixo, como mostrado. Simultaneamente, o conjunto inte
O cursos e o garfo A recebem uma velocidade ascendente constante de 0,2m / s durante um intervalo de movimento e obrigam a esfera na extremidade da barra a deslizar na ranhura radial no disco em rotaç