Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 25

Para a torre e o carregamento do Problema 6.24, sabendo que F C H = F E J = 1,2   k N em C e F E H = 0 , determine a forla no elemento H J e em cada um dos elementos localizados entre H J e N O . Indique se cada elemento está sob tração ou sob compressão.

Passo 1

Vamos começar o exercício analisando o nó G:

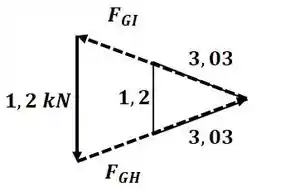
Aplicando semelhança de triângulos entre o triângulo de forças e o de comprimento, temos:

F G I 3,03 = F G H 3,03 = 1,2 1,2

Pegando a primeira e terceira parcelas, temos:

F G I 3,03 = 1,2 1,2 → F G I = 3,03   k N   ( T )

Agora analisando a segunda e terceira parcelas:

F G H 3,03 = 1,2 1,2 → F G H = 3,03   k N   ( C )

Agora vamos analisar o nó L:

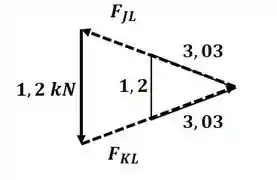
Aplicando semelhança de triângulos entre o triângulo de forças e o de comprimento, temos:

F J L 3,03 = F K L 3,03 = 1,2 1,2

Pegando a primeira e terceira parcelas, temos:

F J L 3,03 = 1,2 1,2 → F J L = 3,03   k N   ( T )

Agora analisando a segunda e terceira parcelas:

F K L 3,03 = 1,2 1,2 → F K L = 3,03   k N   ( C )

Passo 2

Agora vamos analisar o nó J:

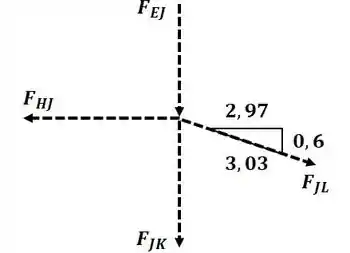
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

- F H J + 2,97 3,03 3,03 = 0 → F H J = 2,97   k N   ( T )

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F J K - 1,2 - 0,6 3,03 3,03 = 0 → F J K = - 1,8   k N → F J K = 1,8   k N   ( C )

Agora vamos analisar o nó H:

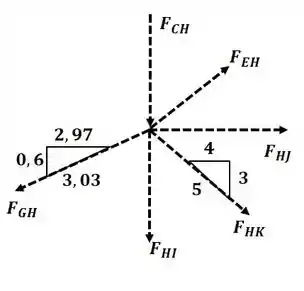
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

4 5 F H K + 2,97 - 2,97 3,03 3,03 = 0 → F H K = 0

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F H I - 1,2 - 0,6 3,03 3,03 - 3 5 0 = 0 → F H I = - 1,8   k N → F H I = 1,8   k N   ( C )

Passo 3

Agora vamos analisar o nó I:

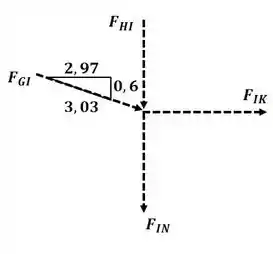
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

F I K + 2,97 3,03 3,03 = 0 → F I K = - 2,97   k N → F I K = 2,97   k N   ( C )

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F I N - 1,8 - 0,6 3,03 3,03 = 0 → F I N = - 2,4   k N → F I N = 2,4   k N   ( C )

Agora vamos analisar o nó K:

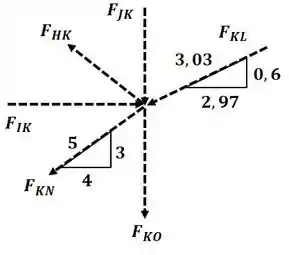
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

- 4 5 F K N + 2,97 - 2,97 3,03 3,03 = 0 → F K N = 0

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F K D - 0,6 3,03 3,03 - 1,8 - 3 5 0 = 0 → F K D = - 2,4   k N → F K D = 2,4   k N ( C )

Resposta

F K D = 2,4   k N ( C )

F K N = 0

F I N = 2,4   k N   ( C )

F I K = 2,97   k N   ( C )

F H I = 1,8   k N   ( C )

F H K = 0

F J K = 1,8   k N   ( C )

F H J = 2,97   k N   ( T )

F K L = 3,03   k N   ( C )

F J L = 3,03   k N   ( T )

F G H = 3,03   k N   ( C )

F G I = 3,03   k N   ( T )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se cada membro da treliça espacial pode sustentar uma força máxima de 600N sob compressão e 800N sob tração, determine a maior força F que a treliça pode sustentar.
Determine a força nos membros E F , D F , C F e C D da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine as componentes horizontal e vertical da reação no pino C .
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
A treliça usada para sustentar um balcão está sujeita às cargas mostradas. Considere cada nó como um pino e determine a força em cada membro. Indique se os membros estão sob tração ou compressão. Faça