Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 26

Resolva o Problema 6.24 considerando que os cabos pendurados no lado direito da torre tenham caído no solo.

Passo 1

Beleza! Comos os cabos pendurados no lado direito caíram no chão, se olharmos para o nó onde estavam pendurados (nó F), veremos que os membros conectados a ele (DF e DE) não possuirão esforços e também os membros ligados ao próximo nó, o nó D, então os membros ligados a D (BD e DE) também não terão esforços associados a eles. Dessa forma:

F D F = F E F = F B D = F D E = 0

Passo 2

Agora vamos analisar o nó A:

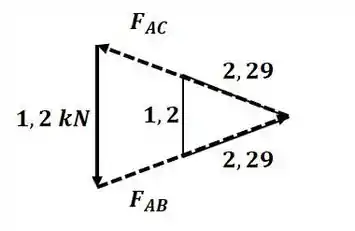
Aplicando semelhança de triângulos entre o triângulo de forças e o de comprimento, temos:

F A B 2,29 = F A C 2,29 = 1,2 1,2

Pegando a primeira e terceira parcelas, temos:

F A B 2,29 = 1,2 1,2 → F A B = 2,29   k N   ( T )

Agora analisando a segunda e terceira parcelas:

F A C 2,29 = 1,2 1,2 → F A C = 2,29   k N   ( C )

Agora vamos analisar o nó B:

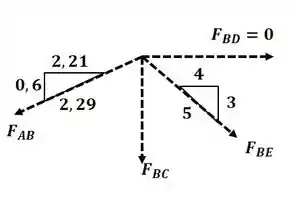
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

4 5 F B E - 2,21 2,29 2,29 = 0 → F B E = 2,76   k N   ( T )

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F B C - 0,6 2,29 2,29 - 3 5 2,76 = 0 → F B C = - 2,26   k N → F B C = 2,26   k N   ( C )

Passo 3

Agora vamos analisar o nó C:

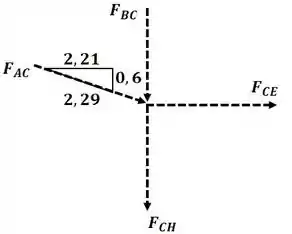
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

F C E + 2,21 2,29 2,29 = 0 → F C E = - 2,21   k N → F C E = 2,21   k N   ( C )

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F C H - 1015 - 0,6 2,29 2,29 = 0 → F C H = - 2,86   k N   C → F C H = 2,86   k N   ( C )

Agora vamos analisar o nó E:

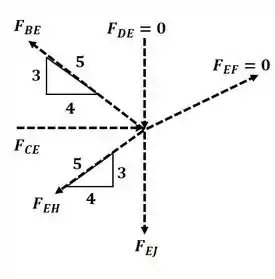
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

- 4 5 F E H - 4 5 2,76 + 2,21 = 0 → F E H = 0

Aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F E J + 3 5 2,76 - 3 5 0 = 0 → F E J = 1,66   k N   ( T )

Resposta

F E J = 1,66   k N   ( T )

F E H = 0

F C H = 2,86   k N   ( C )

F C E = 2,21   k N   ( C )

F B C = 2,26   k N   C

F B E = 2,76   k N   ( T )

F A C = 2,29   k N   ( C )

F A B = 2,29   k N   ( T )

F D F = F E F = F B D = F D E = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força desenvolvida em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. A caixa possui um peso de 750N .
Determine a força nos membros F E e E D da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em C e ligações curtas em A e B .
Determine a força nos membros B E , D F e B C da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , A E , B C , B F , B D e B E da treliça de espaço e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , C D , E D e C F da treliça espacial e indique se os membros estão sob tração ou compressão.