Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 106
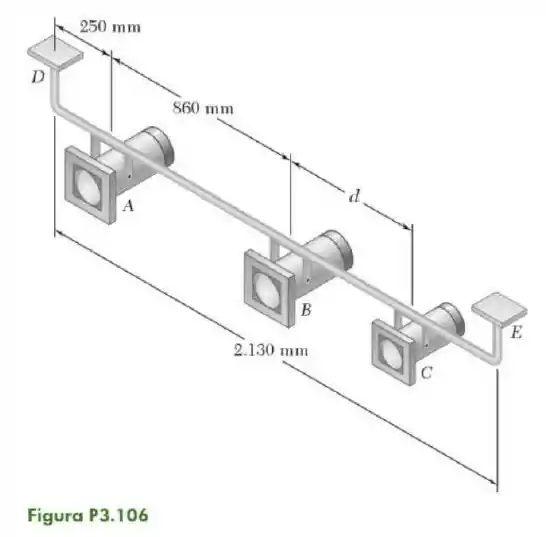
106- Três refletores de palco são montados em um tubo, como mostra a figura. As luzes em e pesam cada uma, enquanto a outra em pesa . Se , determine a distância do ponto até a linha de ação da resultante dos pesos dos três refletores. Determine o valor de de modo que a resultante dos pesos passe pelo ponto médio do tubo.
Passo 1
Como as forças são vetores que apontam somente para baixo então podemos ignorar a distância vertical entre os apoios e com a barra, podendo desenhar.
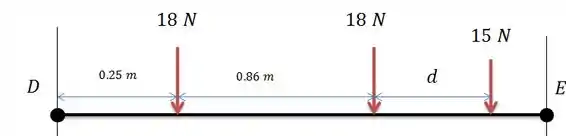
Com as forças descritas no enunciado vemos que a força resultante máxima vale:
E a somatória dos momentos em será:
Para teremos um momento de:
Passo 2
Sabendo que a força resultante gera um momento resultante em de mesmo módulo em há uma distância como na figura abaixo.
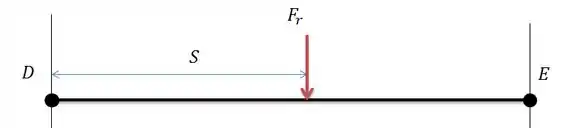
Onde o momento resultante será igual a:
Uma vez que , logo será
Passo 3
Sabendo que na letra está no meio da barra, então :
E como não sabemos o valor de então os dois momentos ficarão: