Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 100
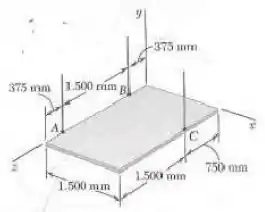
A placa quadrada de peso mostrada na figura é sustentada por três arames verticais. Determine o peso e a localização dos blocos mais leves que poderiam ser colocados na placa se a tração nos três arames for igual.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para resolver este problema, vamos fazer análises com vetores nas três dimensões para facilitar a organização.
Considerando um momento sobre a origem, temos:
Sabendo que:
Vetor posição do ponto .
Vetor posição do ponto .
Vetor posição do ponto .
Vetor posição do centroide .
E e a posição e o peso do bloco de menor peso da situação.
Passo 2
Substituindo os vetores, temos que:
Resolvendo, teremos que:
Agora é só igualar os coeficientes correspondentes. Temos que:
Igualando os coeficientes de , temos que:
Fazendo o somatório de forças em , temos:
Passo 3
Podemos observar que temos três equações e três incógnitas, portanto podemos encontrar os valores desconhecidos rearranjando as equações.
Multiplicando a terceira equação por e somando com a segunda, temos que:
Vamos multiplicar também a terceira equação por e somar com a primeira, para obter:
Passo 4
Agora vamos analisar a relação de cada equação encontrada:
E:
Como o bloco mais leve deve ser colocado na placa, temos que a seguinte condição deve ser respeitada:
Então pensa comigo, se e forem iguais a zero, a relação é mínima.
Logo:
E:
Passo 5
Portanto, teremos que:
Como , temos que:
𝑝𝑚í𝑛=160 N
Logo:
Logo, as coordenadas serão: