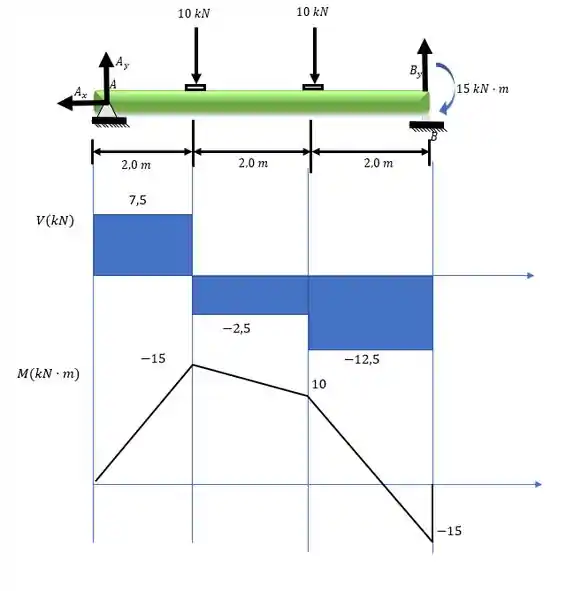
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Passo 1
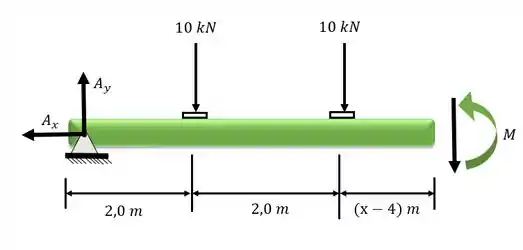
Desenhando o diagrama do corpo livre:
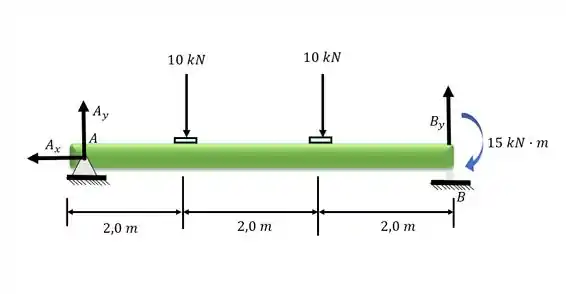
Passo 2
Com o diagrama do corpo livre traçado, podemos calcular as reações de apoio:
Passo 3
Fazendo a análise do cortante e momento fletor para o trecho
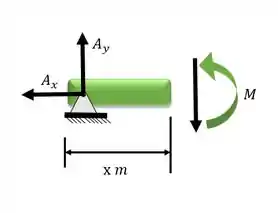
Em relação ao ponto seccionado:
Passo 4
Fazendo a análise do cortante e momento fletor para o trecho
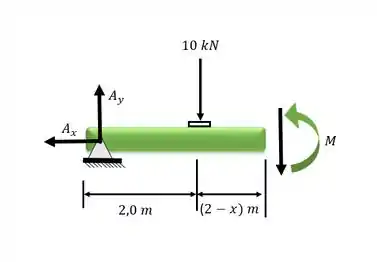
Em relação ao ponto seccionado:
Passo 5
Em relação ao ponto seccionado:
Resposta