Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 10
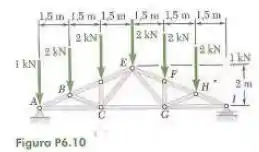
10 Determine a força em cada elemento da treliça de telhado mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Passo 1
Falaaa... beleza??
Vamos começar mandando o diagrama de corpo livre:
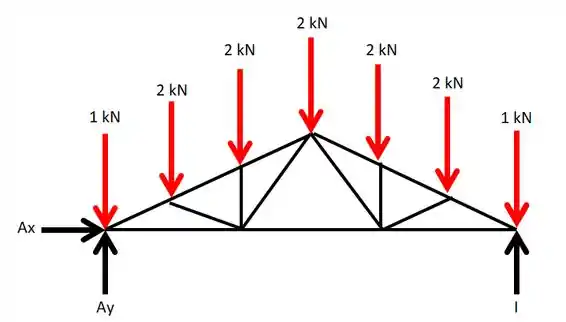
Aplicando o somatório de forças em :
E agora aplicando em :
Pela simetria da treliça:
Então:
Passo 2
Vamos primeiro achar o seno e o cosseno do ângulo que, acredite, vamos usar a beça e também do ângulo :
Pegando o triângulo (ponto é onde bate a altura do ):
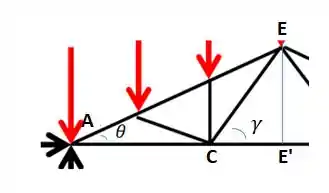
Pra achar :
Para o seno:
E para o cosseno:
E para o ângulo (usando o triângulo ):
Pra achar :
Para o seno:
E para o cosseno:
Passo 3
Vamos analisar a junta A:
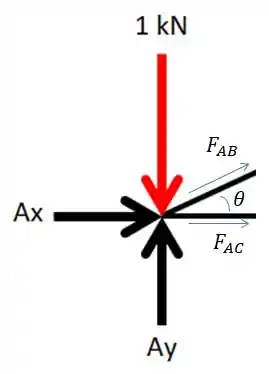
Fazendo o somatório de forças em
E em :
Como é negativa, então é compressão.
Substituindo na de cima:
Como é positiva, então é traçã.
Passo 4
Agora pegando a junta B:
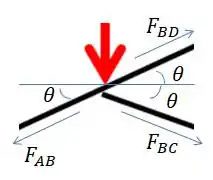
Somatório de forças em :
Em :
Somando as duas equações:
Subtraindo:
Passo 5
Agora a junta D:
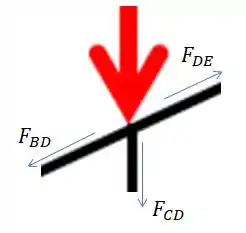
Somatório de forças em :
Somatório de forças em :
Passo 6
Para a junta C:
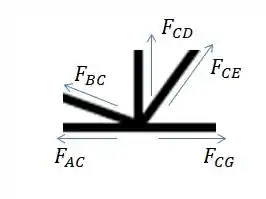
Somatório de forças em :
Somatório de forças em :
Voltando pra equação de :
Passo 7
Da simetria a gente tira todo o resto: