Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 110
110- Para a estrutura e carregamento mostrado na figura, determine a reação em , a força no elemento .
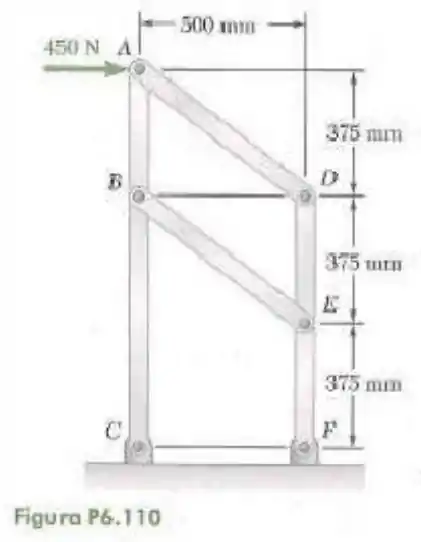
Passo 1
Se analisarmos as forças no corpo todo (retirando a estrutura do chão para expor as forças em e ) nós teremos:
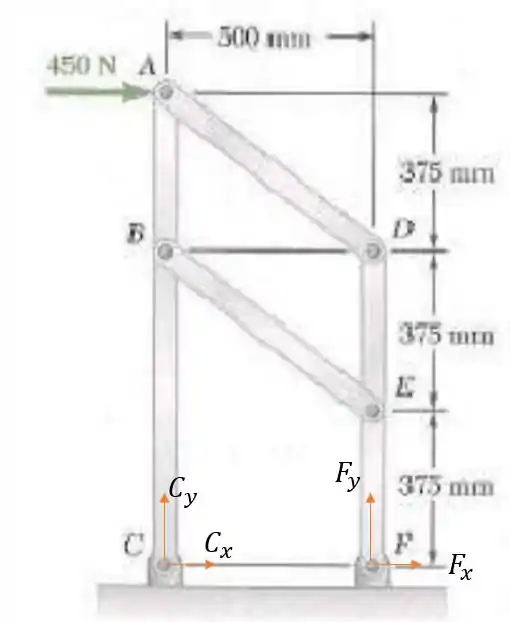
Fazendo a somatória dos momentos em nós temos:
Com isso pela somatória das forças verticais vemos que:
E pela somatória das forças horizontais:
Passo 2
Agora analisando as forças na barra nós temos:
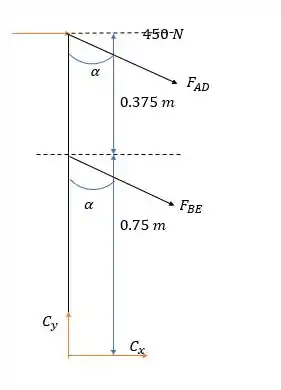
Onde vale:
A somatória dos momentos em serão:
E as forças na barra .
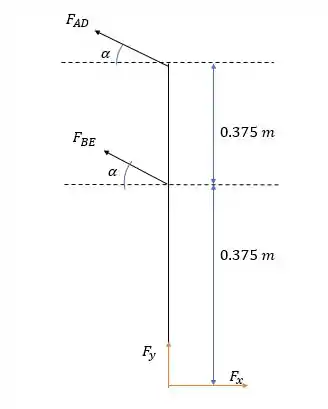
Onde os momentos em seriam iguais a:
Dessa forma a força na barra será:
Força de tração.
Passo 3
Agora precisamos encontrar e para isso vamos voltar de novo para essa figura aqui:
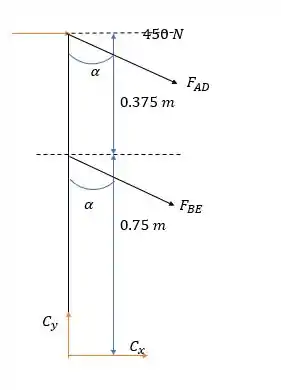
E com isso calcular o momento em .
Logo será:
Dessa forma o módulo de será igual a:
E o ângulo formado com a horizontal será: