Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 9

Determine a força em cada elemento da treliça de telhado Pratt mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.

Passo 1

Beleza! A primeira coisa que devemos fazer é desenhar o diagrama de corpo livre da treliça:

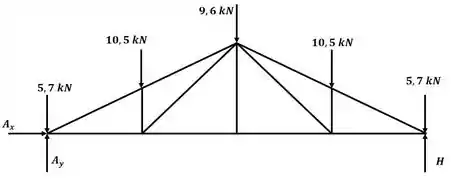
Agora aplicando o somatório de forças na direção :

Devido a simetria desse tipo específico de treliça, o carregamento em está divido igualmente em e , então:

Passo 2

Agora vamos analisar o nó A:

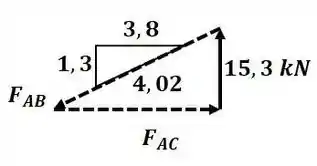
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:

Pegando a primeira e terceira parcela, temos:

Pegando a segunda e terceira parcela, temos:

Agora vamos analisar o nó B:

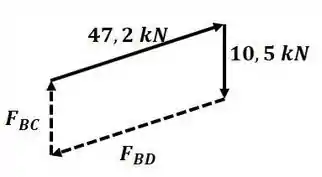
Devido à simetria do paralelogramo de forças, temos que:

Passo 3

Agora vamos analisar o nó C:

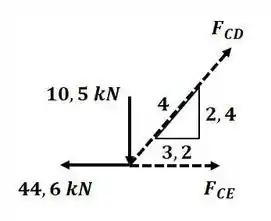
Aplicando o somatório de forças na direção :

Agora aplicando o somatório de forças na direção :

E, por fim, sabemos que esse tipo de treliça possui o membro DE livre de esforço, então:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuando no elemento A B C .

Um binário M de intensidade 1,5 k N ⋅ m é aplicado na manivela do sistema de motor mostrado na figura. Para cada uma das duas posições mostradas, determine a força P necessária para manter o sistema e

Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou compressão.

Usando o método dos nós, determine a força em cada elemento da treliça de passo duplo mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.

38. A treliça mostrada na figura consiste em nove elementos e é sustentada por uma rótula em A , por duas pequenas hastes de conexão em B e uma pequena haste de conexão em C . Determine a força em cad