107. O pião de de raio de giração em relação ao seu eixo de giro de está girando à taxa no sentido indicado, com seu eixo de giro fazendo um ângulo com a vertical. A distância de sua ponta até seu centro de massa é . Determine a pressão do pião e explique porque diminui gradualmente enquanto a velocidade de giro se mantém elevada. Uma vista ampliada do contato na ponta é apresentada.
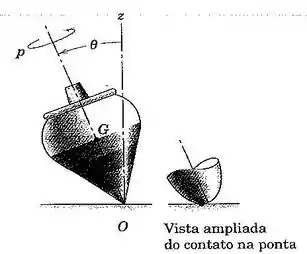
Passo 1
Inicialmente, vamos fazer o esboço do momento de negligência sobre o eixo , isto é, a diminuição do ângulo em comparação com o eixo de rotação:
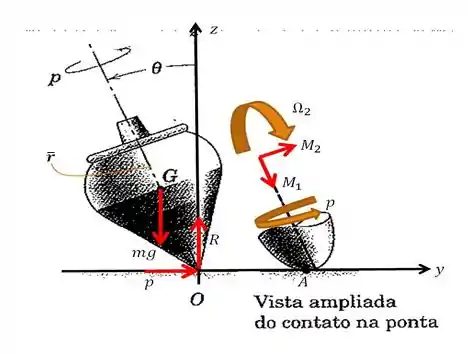
Passo 2
E como já temos os seguintes dados:
Vamos usar a velha e conhecida fórmula:
Só que o nosso da fórmula, ao olhar a imagem bonitinha que fizemos, pode ser escrito como uma decomposição nas direções e :
E ficamos então com:
E , da nossa imagem linda, tiramos que ele encontra-se na direção , portanto com versor , e pode ser escrito como:
E o momento de inércia , para nossa alegria, sabemos que é dado pelo produto do quadrado do eixo de giro pela massa do nosso corpo. Logo:
De modo que obtemos a seguinte relação:
Só nos resta agora, substituir os valores numéricos conhecidos:
E em relação ao fato de que diminui gradualmente enquanto a velocidade de giro se mantém elevada, temos que é porque a força de atrito em A que está no papel, no eixo , produz um momento , para aumentar a velocidade rotação e um momento , que é responsável por causar a precessão que diminui . Esses momentos estão ilustrados na nossa bela imagem.