Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 65

O cone circular reto de altura h e raio da base r gira em torno de seu eixo de simetria com uma velocidade angular p . Simultaneamente, o cone inteiro gira em torno do eixo x com velocidade angular Ω . Determine a quantidade de movimento angular H o do cone em relação à origem O dos eixos x - y - z e a energia cinética T para a posição mostrada. A massa do cone é m .

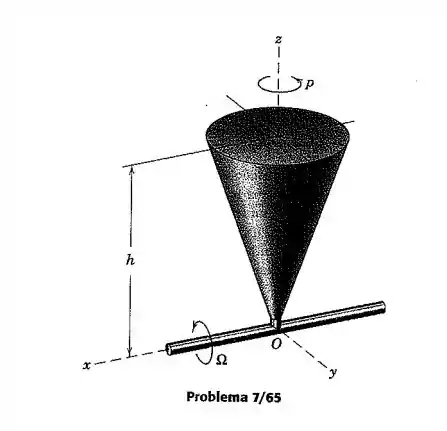
Passo 1

Para resolvermos o exercício proposto, vamos precisar calcular os tensores de inércia do cilindro reto e depois utilizaremos a equação da quantidade de movimento angular H o para descobrirmos qual a energia cinética de rotação

Passo 2

Vamos começar calculando as componentes do tensor de inércia. Para obtermos os valores será necessário calcular as seguintes integrais:

I x x = ∭ y 2 + z 2 ⋅ ρ ⋅ d V

I z z = ∭ x 2 + y 2 ⋅ ρ ⋅ d V

I x y = ∭ x ⋅ y ⋅ ρ ⋅ d V

Sabemos, pela simetria do problema, que I x x = I y y e I x y = I y z = I x z . Resolvendo as integrais, chegaremos que

I x x = I y y = 3 20 ⋅ m ⋅ r 2 + 3 5 ⋅ m ⋅ h 2

I z z = 3 10 ⋅ m ⋅ r 2

I x y = I y z = I x z = 0

Utilizando agora a equação para H o , temos que:

H o = I x x ⋅ ω x ⋅ i + I y y ⋅ ω y ⋅ j + I z z ⋅ ω z ⋅ k

O problema nos fala que ω x = Ω , ω y = 0 e ω z = p . Assim, teremos que

H o = I x x ⋅ ω x ⋅ i + I z z ⋅ ω z ⋅ k

H o = 3 20 ⋅ r 2 + 3 5 ⋅ h 2 ⋅ m ⋅ Ω ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ k

Passo 3

Para encontrarmos a energia cinética do sistema, basta substituirmos o valor de H 0 na seguinte equação

T = 1 2 ⋅ ω ⋅ H o = 1 2 ⋅ Ω ⋅ i + p ⋅ k ⋅ [ 3 20 ⋅ r 2 + 3 5 ⋅ h 2 ⋅ m ⋅ ] Ω ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ k ]

T = 3 10 ⋅ m ⋅ r 2 ⋅ 1 4 + h 2 r 2 ⋅ Ω 2 + 1 2 ⋅ p 2

Resposta

H o = 3 20 ⋅ r 2 + 3 5 ⋅ h 2 ⋅ m ⋅ Ω ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ k

T = 3 10 ⋅ m ⋅ r 2 ⋅ 1 4 + h 2 r 2 ⋅ Ω 2 + 1 2 ⋅ p 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

146. Desenvolva a Eq. 7 / 24 , relacionando as forças às acelerações para um elemento diferencial do anel fino de massa m . O anel possui uma velocidade angular constante p em torno do eixo z e recebe
142. O desbalanceamento dinâmico de um determinado virabrequim é aproximado pela modelo físico apresentado, onde o eixo sustenta três esferas pequenas de 0,6k g fixadas por hastes de massa desprezível
144. Cada uma das placas com o formato de um quadrante de círculo possui uma massa de 2k g e está presa ao eixo vertical montado no mancal fixo em O . Calcule o módulo M do momento fletor no eico em O
O carrinho e sua carga têm uma massa total de 100k g . Determine a aceleração do carrinho e as reações normais sobre o par de rodas em A e B . Despreze a massa das rodas.
No instante mostrado, ambas as barras de massa desprezível balançam com uma velocidade angular no sentido anti-horário ω = 5r a d / s , enquanto a barra de 50k g está sujeita à força horizontal de 100