Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 59

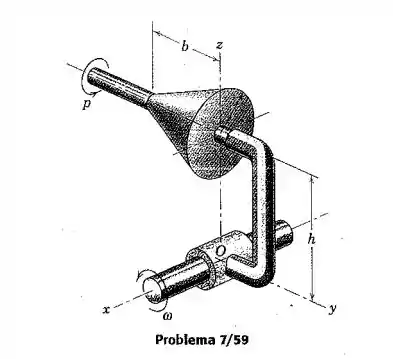
O cone circular reto maciço de massa m , comprimento b , e raio da base r gira a uma velocidade angular p em torno de seu eixo de simetria. Simultaneamente, o suporte e o eixo da haste anexa giram na taxa ω em torno do eixo x . Determine a quantidade de movimento angular H o do cone em relação ao ponto O e sua energia cinética T .

Passo 1

Para esse problema, vamos usar a relação para quantidade de movimento angular H o e os dados da tabela D/4 para obtermos dois termos do tensor de inércia. Após isso, substituiremos todos os valores obtidos na equação de H o para obtermos a energia cinética do sistema.

Passo 2

Inicialmente, temos pela tabela D/4, que I x x = I z z = 3 20 ⋅ m ⋅ r 2 + 3 80 ⋅ m ⋅ b 2 . Para a última componente, precisamos calcular a seguinte integral para obter seu valor

I y y = ∭ x 2 + z 2 ⋅ ρ ⋅ d V = 3 10 ⋅ m ⋅ r 2

Temos que a equação de H o pode ser escrita da seguinte forma:

H o = H G + r × m ⋅ v

Onde r é a distância até o centro de massa do cone, que é localizado em - b 4 . Assim, r = h ⋅ k - b 4 ⋅ j , e derivando essa relação, chegamos que a velocidade do centro de massa será v = - h ⋅ ω ⋅ j - b 4 ⋅ ω ⋅ k

Vamos calcular agora o produto vetorial r × m ⋅ v :

r × m ⋅ v = b 2 16 ⋅ ω ⋅ m ⋅ i + h ⋅ b 4 ⋅ ω ⋅ m ⋅ j + h 2 ⋅ ω ⋅ m ⋅ k

r × m ⋅ v = m ⋅ ω ⋅ b 2 16 ⋅ i + h ⋅ b 4 ⋅ j + h 2 ⋅ k

Temos que H G = I x x ⋅ ω x ⋅ i + I y y ⋅ ω y ⋅ j + I z z ⋅ ω z ⋅ k . Onde ω x = ω , ω y = p e ω z = 0 como dado no enunciado. Substituindo esses valores em H G , temos que:

H G = 3 20 ⋅ m ⋅ r 2 + 3 80 ⋅ m ⋅ b 2 ⋅ ω ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ p ⋅ k

Substituindo os valores em H o chegamos que

H o = m ⋅ ω ⋅ 3 20 ⋅ r 2 + 1 10 ⋅ b 2 + h 2 ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ p ⋅ j

Passo 3

Para a energia cinética basta substituirmos na relação

T = 1 2 ⋅ ω ⋅ H o = 1 2 ⋅ m ⋅ ω 2 ⋅ 3 20 ⋅ r 2 + 1 10 ⋅ b 2 + h 2 + 3 2 0 ⋅ m ⋅ r 2 ⋅ p 2

Resposta

H o = m ⋅ ω ⋅ 3 20 ⋅ r 2 + 1 10 ⋅ b 2 + h 2 ⋅ i + 3 10 ⋅ m ⋅ r 2 ⋅ p ⋅ j

T = 1 2 ⋅ m ⋅ ω 2 ⋅ 3 20 ⋅ r 2 + 1 10 ⋅ b 2 + h 2 + 3 20 ⋅ m ⋅ r 2 ⋅ p 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

119. Um menino lança um disco circular fino (como um F r i s b e e ) com uma velocidade de giro de 300r p m . Observa-se o plano do disco oscilar através de um ângulo total de 10 ° . Calcule o período
118. Os dois discos circulares idênticos, cada um de massa m e raio r , estão girando com uma unidade rígida em torno de seu eixo comum. Determine o valor de b para o qual não ocorrerá movimento de pr
120. A figura mostra uma bola de futebol americano em três configurações comuns durante o vôo. O caso (a) é um passe em espiral arremessado perfeitamente com uma velocidade de giro de 120r p m . O cas
125. Os dois cones circulares retos homogêneos maciços, cada um de massa m , são fixados um ao outro em seus vértices para formar uma unidade rígida e estão girando em torno de seu eixo de simetria ra
124. O satélite de observação da Terra está em uma órbita circular de período τ . A velocidade angular do satélite em torno de seu eixo y ou eixo de arfagem é ω = 2 π / τ , e as velocidades angulares