Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 67

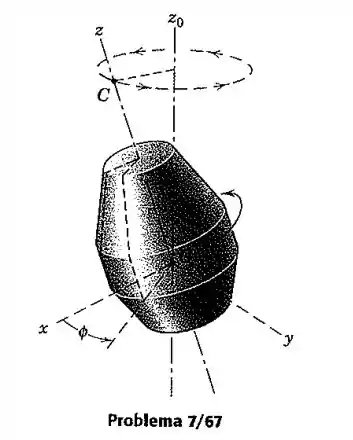
A nave espacial mostrada possui uma massa m com centro de massa G . Seu raio de giração em relação a seu eixo z de simetria rotacional é k e em relação a ambos os eixos x ou y é k ' . No espaço, a nave espacial gira no interior de seu sistema de referência x - y - z à taxa p = ϕ . Simultaneamente, um ponto C sobre o eixo z se desloca em um círculo em torno do eixo z 0 com uma frequência f (rotações por unidade de tempo). O eixo z 0 possui uma direção constante no espaço. Determine a quantidade de movimento angular H G da nave espacial em relação aos eixos indicados. Observe que o eixo x se situa sempre no plano z - z 0 e que o eixo y é consequentemente perpendicular a z 0 .

Passo 1

Para resolvermos o exercício proposto, vamos precisar encontrar as velocidades angulares de giro do eixo e após isso, vamos precisar encontrar a velocidade angular total do sistema, além de relacionar a velocidade angular com a frequência.

Passo 2

Vamos começar coletando as informações que o enunciado nos dá. Temos que os momentos de inércia serão I x x = m ⋅ k ' 2 , I y y = 0 e I z z = m ⋅ k 2 . Temos que H G = I x x ⋅ ω x + I y y ⋅ ω y + I z z ⋅ ω Z , logo precisamos encontrar as componentes do vetor ω , que será a velocidade angular do sistema.

Podemos escrever ω como soma de todas as velocidades do sistema, logo

ω = Ω + p .

Onde Ω é a velocidade angular do eixo e p uma velocidade qualquer que esteja no sistema. Observando a esquematização do problema, vemos que a velocidade angular Ω pode ser decomposta em velocidades angulares para cada eixo, ficando da seguinte forma

Ω x = - Ω ⋅ sin ⁡ θ

Ω y = 0

Ω z = Ω ⋅ cos ⁡ θ

Assim, as componentes da velocidade ω serão ω x = - Ω ⋅ sin ⁡ θ , ω y = 0 e ω z = Ω ⋅ cos ⁡ θ + p . Substituindo na equação de H G , chegaremos a

H G = - m ⋅ k ' 2 ⋅ Ω ⋅ sin ⁡ θ ⋅ i + m ⋅ k 2 ⋅ Ω ⋅ cos ⁡ θ + p ⋅ k

Mas, temos pelo enunciado a frequência com que os eixos giram e sabemos que é possível escrever a velocidade angular em termos da frequência pela equação Ω = 2 ⋅ π ⋅ f . Substituindo, ficamos então com

H G = - m ⋅ k ' 2 ⋅ 2 ⋅ π ⋅ f ⋅ sin ⁡ θ ⋅ i + m ⋅ k 2 ⋅ 2 ⋅ π ⋅ f ⋅ cos ⁡ θ + p ⋅ k

H G = 2 ⋅ π ⋅ f ⋅ m ⋅ - k ' 2 ⋅ sin ⁡ θ ⋅ i + k 2 ⋅ cos ⁡ θ + m ⋅ k 2 ⋅ p ⋅ k

Resposta

H G = 2 ⋅ π ⋅ f ⋅ m ⋅ - k ' 2 ⋅ sin ⁡ θ ⋅ i + k 2 ⋅ cos ⁡ θ + m ⋅ k 2 ⋅ p ⋅ k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

128. Se o navio do Exemplo 7 / 8 está em curso reto, mas a sua proa está abaixando enquanto cai no vale de uma onda, determine o sentido do momento giroscópico exercido pelo rotor da turbina sobre a e
129. Um carro experimental é equipado com um estabilizador giroscópico para neutralizar completamente a tendência do carro a inclinar ao realizar uma curva (sem variação na força normal entre os pneus
127. A casca cilíndrica está girando no espaço em torno de seu eixo geométrico. Se o eixo sofre uma ligeira oscilação, para quais razões de l / r o movimento será de precessão direta ou retrógrada?
145. Calcule o momento fletor M no eixo O para o conjunto em rotação do Prob 7 / 144 , quando parte do repouso com uma aceleração angular inicial de 200r a d / s 2 .
143. Cada uma das duas barras dobradas em ângulo reto possui uma massa de 1,2k g e é paralela ao plano horizontal x - y . As barras estão soldadas à haste vertical, que gira em torno do eixo z com uma