97. Os elementos da suspensão traseira independente, do tipo “eixo-flutuante”, para automóveis são representados na figura. O diferencial está firmemente fixado ao chassi do carro. Os semieixos são articulados em suas extremidades internas (ponto para o semieixo mostrado) e estão firmemente presos às rodas. Os elementos da suspensão não mostrados limitam o movimento da roda ao plano da figura. A massa do conjunto roda-pneu é , e seu momento de inércia de massa em relação a um eixo diametral que passa através de seu centro de massa é de . A massa do semieixo é desprezível. A constante da mola e o coeficiente de amortecimento do amortecedor são e , respectivamente. Se um desbalanceamento estático está presente no pneu, tal como representado pela massa concentrada adicional como apresentado , determine a velocidade angular , que resulta no sistema de suspensão sendo excitado em sua frequência natural não amortecida. Qual seria a velocidade correspondente do veículo ? Determine o fator de amortecimento . Assuma pequenos deslocamentos angulares e despreze os efeitos giroscópicos e qualquer vibração do chassi do carro. A fim de evitar as complicações associadas com a variação da força normal exercida pela estrada sobre o pneu, considere o veículo como posicionado sobre um elevador com as rodas suspensas livremente.
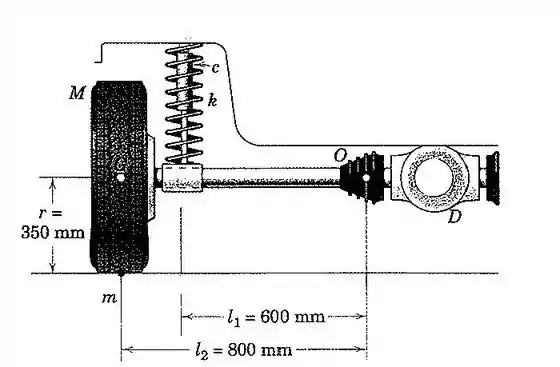
Passo 1
Primeiro, vamos montar o diagrama da haste com a roda:
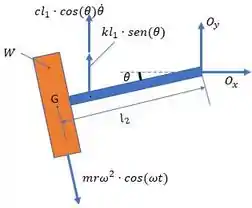
Passo 2
Agora, vamos calcular o momento de inércia do sistema em relação ao ponto usando o teorema dos eixos paralelos:
Passo 3
Em seguida, vamos fazer a soma de momentos em relação ao ponto :
Para pequeno, temos e
Rearranjando a equação:
Passo 4
A equação genérica de um movimento harmônico amortecido e forçado é dado por:
Dessa forma, podemos calcular como:
Passo 5
Agora, vamos achar a velocidade correspondente do veículo :
Passo 6
E finalmente para achar o fator de amortecimento , vamos utilizar a relação:
Resposta
A velocidade angular será:
A velocidade :
E o fator de amortecimento: