Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 109
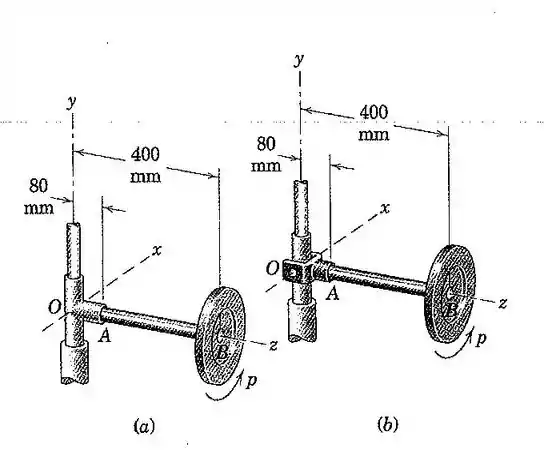
109. Cada uma das rodas idênticas tem uma massa de e um raio de giração e está montada a uma haste horizontal presa à haste vertical em . No caso (a), a a haste horizontal está fixada a uma luva em , que é livre para girar em torno do eixo vertical. No caso (b), a haste está presa a luva por um garfo articulado em torno do eixo . Se aroda possui uma velocidade angular elevada em torno de seu eixo na posição mostrada, determine qualquer precessão que ocorra e o momento fletor na haste para cada caso. Despreze a pequena massa da haste e da conexão em .
Passo 1
(a) Inicialmente, vamos fazer o esboço das forças e momentos atuantes no nosso sistema, para analisar como pede a questão, se há ou precessão. Segue abaixo, a nossa obra de arte para o primeiro caso:
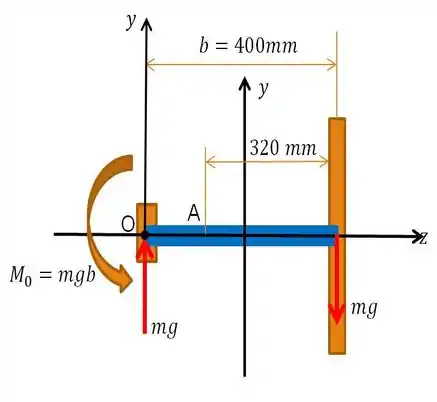
E o que vem em seguida é moleza! Temos que nesse caso não irá ocorrer precessão, uma vez que a linha de atuação de nosso esforços é de que não corresponde a haste toda. Para encontrar o momento fletor correspondente basta fazer o somatório das forças na direção igual a zero, que são o somatório dos momentos em que a linha de atuação está naquela distância de , ou seja:
Passo 2
(b) E agora, façamos o esboço dos esforços atuantes para o segundo caso, em que a haste vai estar presa a luva por um garfo articulado em torno do eixo . Vamos incluir no nosso desenho, o giro e a representação da direção da precessão :
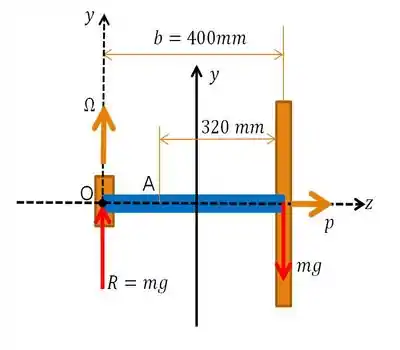
Nesse caso ocorre precessão uma vez que a linha de atuação de nossos esforços é toda distância de . Com isso, bora fazer com que o somatório das forças na direção , seja igual a zero. Só que dessa vez, a nossa distância para o cálculo do momento vai ser igual a ou seja:
E se temos o momento, não podemos esquecer que ele está relacionado ao momento de inércia e à precessão pela seguinte fórmula, considerando é claro que eles estão em direções ortogonais, de modo que nem precisamos fazer o produto vetorial:
Olha só que beleza. A questão já nos forneceu que o raio de giração é igual a . Podemos reescrever a fórmula de então, como:
E como sabemos os valores numéricos:
Bora tratar de substituir na fórmula, pois tá na cara que é a precessão que iremos obter:
Por fim, não podemos nos esquecer que a questão pede também o momento fletor na haste para essa caso! Para isso, vamos analisar o trecho da nosssa haste:
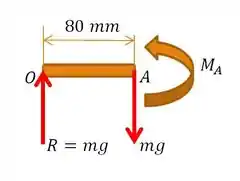
O momento fletor, que cuja notação é , através dessa bela imagem, tiramos que ele é dado por:
Resposta
(a)
(b)