Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 85
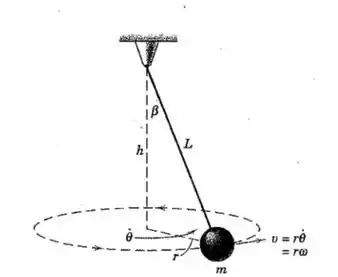
A pequena esfera de massa está presa a um fio leve de comprimento e se desloca como um pêndulo cônico em um círculo horizontal com uma velocidade tangencial . Localize o plano de movimento pela determinação de , e encontre a tração no fio. (Observação: Utilize a relação , onde é a velocidade angular em torno do eixo vertical.)
Passo 1
Vamos pensar nas forças envolvidas aqui. Temos uma tração direcionada ao longo do fio e o peso apontando na vertical para baixo como sempre.
Então na vertical temos:
E na horizontal temos:
Beleza, na vertical as forças precisam se cancelar, já que a esfera não tem nenhum movimento nessa direção, e na horizontal precisamos de uma resultante centrípeta:
Ok, então temos o seguinte sistema:
Passo 2
Dividindo a segunda equação pela primeira:
E como podemos usar isso para encontrar o valor de ? Bom olhando para a figura podemos ver que:
E essa altura já define a posição do plano de movimento!
Passo 3
E agora podemos encontrar a tensão de várias formas. Por exemplo, olhando de novo para a figura podemos ver que:
E olhando para a primeira equação do nosso sistema:
Pronto!
Resposta
e .