Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 229

O centro de massa G da pessoa de 70 kg mostrada tem uma velocidade máxima de 4 m/s na posição mais baixa do balanço. Para as dimensões dadas, calcule o momento fletor M suportado pelas vértebras lombares da coluna para essa posição. A vértebra lombar do meio e o centro de massa G do corpo são praticamente coincidentes. O centro de massa da parte inferior do corpo está em G 1 para o posição mostrada. Assuma que as massas das partes superior e inferior do corpo são iguais. Despreze também a massa do balanço e a massa dos braços da pessoas.

Passo 1

Primeiramente é necessário determinar o DCL do corpo em analise, confomer a figura abaixo mostra.

∑ F t = m a t

R s i n 18 ° - F t = m 2 v 2 ρ s i n ⁡ ( α )

α = sin - 1 ⁡ 0,325 2,3 = 8,12 °  

903   s i n 18 ° - F t = 70 2 4 2 2,3 s i n ⁡ ( 8,12 ° )

903   s i n 18 ° - F t = 70 2 4 2 2,3 s i n ⁡ ( 8,12 ° )

F t = 244,65   N

↻ ∑ M o = 0

903 sin ⁡ 18 ° 2,3 - 0,455 - 35 ( 9,81 ) 0,325 + 244,65 2,3 + M = 0

M = 58,4   N ∙ m

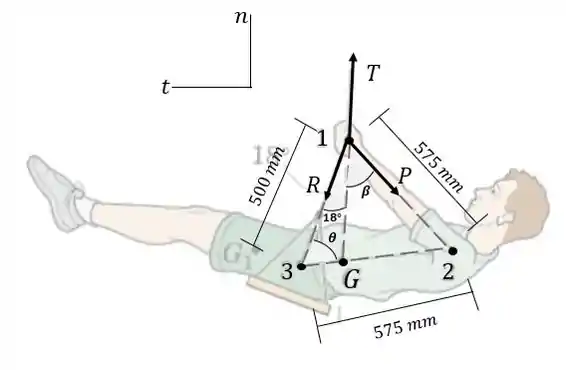
Passo 2

Para os somatório de forças

∑ F n = m a n

T - P e s o = m v 2 ρ

T - 70 ( 9,81 ) = 70 4 2 2,3

T = 1173,66   N

θ = cos - 1 ⁡ 250 575 = 64,2 °

β = θ - 18 ° = 46,2 °

∑ F n = 0

T - R c o s 18 ° - P c o s 46,2 ° = 0

R s i n 18 ° - P c o s 46,2 ° = 0

P = 385,77   N

R = 902,99   N

Passo 3

Para calcular o momento fletor M suportado pelas vértebras lombares da coluna para essa posição é necessário um segundo DCL com parte inferior do corpo. Mostrado na figura abaixo

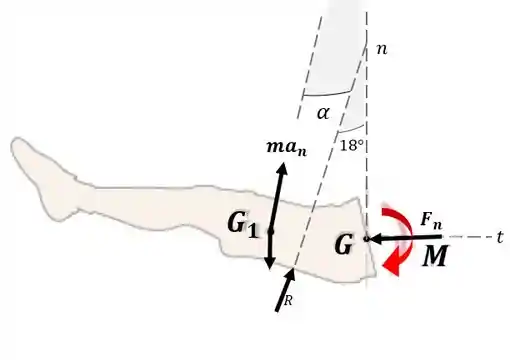
E novamente é feito o somatório de momentos e forças,

∑ F t = m a t

R s i n 18 ° - F t = m 2 v 2 ρ s i n ⁡ ( α )

α = sin - 1 ⁡ 0,325 2,3 = 8,12 °  

903   s i n 18 ° - F t = 70 2 4 2 2,3 s i n ⁡ ( 8,12 ° )

903   s i n 18 ° - F t = 70 2 4 2 2,3 s i n ⁡ ( 8,12 ° )

F t = 244,65   N

↻ ∑ M o = 0

903 sin ⁡ 18 ° 2,3 - 0,455 - 35 ( 9,81 ) 0,325 + 244,65 2,3 + M = 0

M = 58,4   N ∙ m

Resposta

O momento fletor é M = 58,4   N ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O volante A de 15 kg tem um raio de giração em relação a seu centro de 100 mm. O disco B tem uma massa de 25 kg e está acoplado ao volante através de uma correia que não desliza em suas superfícies de
O corpo rígido (placa) tem uma massa m e gira com uma velocidade angular ω em relação a um eixo passando pelo ponto fixo O. Demonstre que os momentos de todas as partículas compondo o corpo podem ser
O volante A tem uma massa de 30 kg e um raio de giração k C = 95m m . O disco B tem uma massa de 25 kg, está preso com pino em D, e está acoplado ao volante usando uma correia que está submetida a uma
O disco circular de 25 kg está fixado ao garfo através de um eixo liso A. O parafuso C é usado para travar o disco ao garfo. Se o garfo é submetido a um torque M = 5 t 2N . m , onde t é dado em segund
O ginasta de 75 kg solta a barra horizontal em uma posição completamente deformada A, girando com uma velocidade angular ω A = 3r a d / s . Estime sua velocidade angular quando ele assume uma posição