Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 123

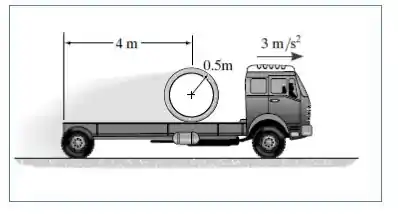
O duto de concreto de 500 kg tem um raio médio de 0,5 m. Se o caminhão tem uma aceleração 3 m/s², de termine a aceleração angular do duto. Supondo que o duto não deslize sobre o piso da carroceria do caminhão e despreze sua espessura.

Passo 1

Definir as equações de movimento:

  ↺ + Σ M G = Σ M k A ; 0 = 125 a -   500 a g 0,5

Passo 2

Assumindo que não deslizamento e aplicando a equação de aceleração relativa:

a g = a A + a   x   r G / A -   ω ² r G / A

a g i = 3 i + a A j + a k   x   0,5 j -   ω ² ( 0,5 j )

a g i = 3 - 0,5 a i + a A - 0,5   ω 2 j

Passo 3

Resolvendo o sistema.

125 a = 500 a g

a g = 3 - 0,5 a

Primeiro deixaremos em termos de a .

500 a g 125 = a

Substituindo na equação II :

a g = 3 - 0,5.500 a g 125

Isolando para a g :

a g = 1,5 m / s ²

Então:

a = 3   r a d / s ²

Resposta

Assim a aceleração a g = 1,5   m / s 2 e a aceleração a = 3   r a d / s ² .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um rolo de papel de 17 kg, originalmente em repouso, é apoiado pelo apoio AB. Se o rolo repousa contra uma parede onde o coeficiente de atrito cinético é μ C = 0,3 , e uma força constante de 30 N for
O volante de 50 kg tem um raio de giração em relação a seu centro de massa k O = 250m m . Ele gira com uma velocidade angular constante de 1200 rev/min antes de o freio ser aplicado. Se o coeficiente
A bobina de 200 kg tem um raio de giração em relação a seu centro de massa k G = 300m m . Se o momento de binário é aplicado à bobina e o coeficiente de atrito cinético entre a bobina e o solo é μ k =
O cilindro de 100 kg rola sem deslizar sobre o plano horizontal. Determine a aceleração de seu centro de massa e sua aceleração angular.
A barra fina uniforme de 60 kg está inicialmente em repouso sobre um plano horizontal liso quando as forças são aplicadas. Determine a aceleração do centro de massa da barra e a aceleração angular da