Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 11

11- A garra superior D da prensa desliza sem atrito ao longo da coluna vertical fixa. Determine a força F necessária sobre a manopla, para produzir uma compressão R sobre o rolamento para qualquer valor dado de θ .

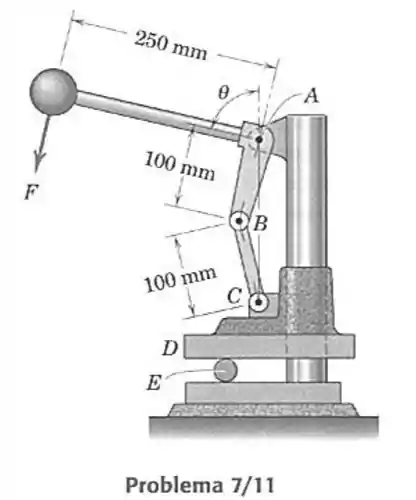
Passo 1

Fazendo o sistema de forças do sistema acima teremos:

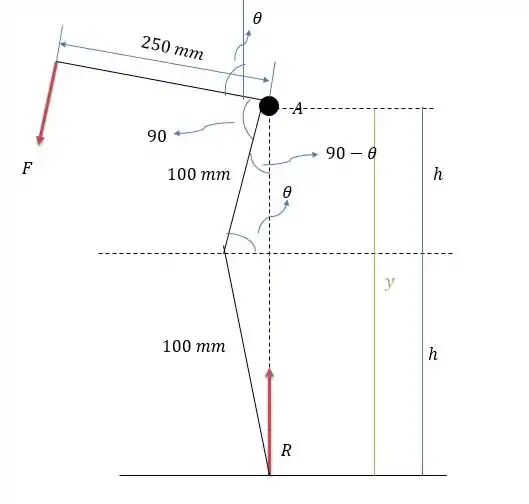
A força F faz o ângulo θ aumentar, logo o trabalho virtual causado por essa força é o momento no eixo de 250   m m ou 0.25   m que será de :

δ U F = F × 0.25 × δ θ

E o trabalho causado pela força que surge na máquina de intensidade R será de:

δ U R = - R δ y

Já que ela tende a comprimir a reta y .

Logo a somatória dos trabalhos virtuais será de:

δ U = δ U F + δ U R = 0.25 F δ θ - R δ y = 0

Passo 2

No enunciado não fala, mas o desenho leva a crer que o ângulo F A B   é de 90 graus, então fazendo o rebatimento dos ângulos conseguimos encontrar um ângulo de 2 θ em A B C . Logo a altura h que vale y / 2 será de :

sin ⁡ θ = h 0.1 → h = 0.1 sin ⁡ θ

y = 2 h

y = 0.2 sin ⁡ θ

Substituindo esse valor na somatória de trabalhos virtuais nós vamos ter:

0.25 F δ θ - R δ ( 0.2 sin ⁡ θ ) = 0

0.25 F δ θ = 0.2 R cos ⁡ θ   δ θ  

Cortando δ θ :

0.25 F = 0.2 R c o s   θ

Isolando F :

F = 0.2 R c o s   θ 0.25 = 0.8 R c o s   θ

Resposta

F = 0.8 R c o s   θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16. Deduza uma expressão para a intensidade do binário M necessária para se manter o equilíbrio do mecanismo articulado mostrado na figura.
17. Deduza uma expressão para a intensidade do binário M necessária para se manter o equilíbrio do mecanismo articulado mostrado na figura.
4. Determine o binário M que deve ser aplicado ao elemento A B C para se manter o equilíbrio do sistema articulado.
6. O mecanismo articulado de duas barras mostrado na figura é sustentado por um pino e um suporte em B e por um colar em D , que desliza livremente sobre uma haste vertical. Determine a força P necess
7. Uma mola de constante 15N / c m é presa a pinos nos pontos C e F tal como mostra a figura. Desprezando o peso da mola e do mecanismo articulado, determine a força na mola e o deslocamento vertical