Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 51

51- Uma extremidade da mola de torção está presa ao chão em A e a outra extremidade está presa ao eixo em B . A rigidez a torção K da mola elástica é o torque necessário para torcer a mola de um ângulo de um radiano. A mola resiste ao momento em torno do eixo, causado pela força de tração m g no cabo enrolado ao redor do tambor de raio r . Determine o valor de equilíbrio de h medido a partir da posição tracejada, na qual a mola está torcida.

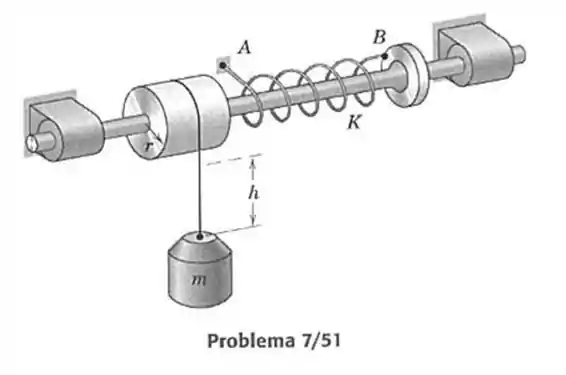
Passo 1

O enunciado e a figura da questão nos apresentam duas energias, a potencial gravitacional causada pela massa e a energia potencial elástica. Tal qual podemos desenhar a seguinte figura.

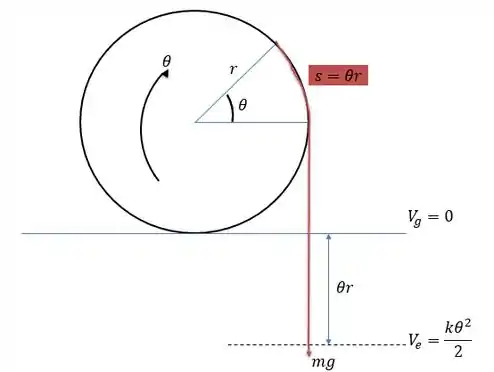
Se rodarmos o tambor em um ângulo θ vemos que a corda desce o tambor com o mesmo comprimento do arco s que a corda forma com o tambor e que terá valor igual a :

s = h = θ r

E essa descida de corda faz o tambor girar e fazer com que surja uma energia potencial elástica torcional. Logo a energia potencial gravitacional do sistema será:

V g = - m g θ r

Negativo já que a corda está abaixo da linha de energia nula.

E a energia potencia elástica será:

V e = 1 2 k θ 2

Logo a energia total do sistema será:

V = - m g r θ + 1 2 k θ 2

Passo 2

Derivando uma vez a expressão da energia em relação a θ nós teremos:

d V d θ = - m g r + k θ

Igualando a zero nós encontramos a posição de equilíbrio.

- m g r + k θ = 0

k θ = m g r

Como h = r θ logo θ = h r , até por que nos interessa eliminar o valor de θ pois é uma variável não existente no enunciado, logo:

k h r = m g r

Isolando h :

h = m g r 2 k

Resposta

h = m g r 2 k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 30 .
Um carro que pesa 75N rola na rampa que faz um ângulo com a hotizontal. Sabendo que k = 5 k N / m e que a mola está indeformada quando x = 0 , determine a distância x para equilíbrio quando β = 6 0 .
A mola AB, de constante k , está indeformada quando θ = 0 , determine (a) os intervalos de θ para equilíbrio estável e (b) dois valores para equilíbrio tal que P é metade do limite superior encontrado
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .
A haste AB está presa a uma articulação em A e a duas molas, cada qual de constante k. Se h = 625 mm, d -=300 mm e W = 360 N, determine o intervalo de valores dc k para os quais o equilíbrio da haste