Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 52
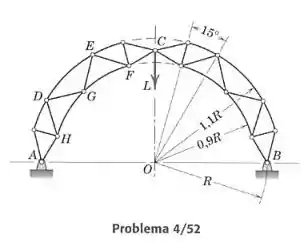
Determine a força no elemento da treliça composta. Todas as juntas se situam em linhas radiais subentendendo ângulos de 15° como indicado, e os elementos curvos agem como elementos de duas forças. Distância .
Passo 1
Vamos calcular a força pelo método das seções, traçando um corte na treliça e fazendo as equações de equilíbrio para uma parte dele como se fosse um corpo rígido. Como estamos interessados no elemento , fazemos um corte passando por , e . A parte que sobra é mostrada na figura:
Para aplicarmos as equações de equilíbrio do corpo rígido precisamos primeiramente da força vertical em . Pela simetria do sistema, a força aplicada em e são iguais, e o valor deve ser para cima, para que as duas anulem a força para baixo aplicada no meio da treliça. Agora precisamos obter os ângulos que as forças fazem com a horizontal para resolver o problema.
Passo 2
Para encontrar os ângulos e , desenhamos os triângulos e .
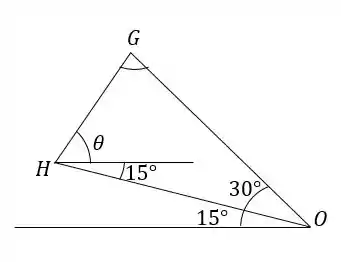
Como o triângulo é isósceles, o ângulo que não é o de 30° vale:
Achamos da mesma forma:
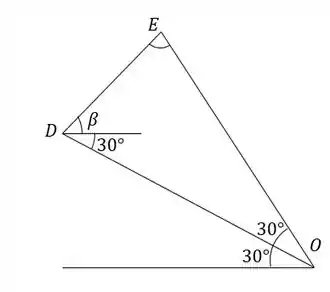
Não podemos achar da mesma maneira, então precisamos das coordenadas dos pontos em relação à origem O. Os pontos envolvidos são D e G. G está no círculo de raio 0,9R, sendo o ângulo entre OG e a horizontal 45°. Então:
D está num círculo de raio 1,1R. OD faz 30° com a horizontal. Então:
Agora podemos encontrar o ângulo, através de sua tangente. Temos:
Passo 3
Agora já temos os dados necessários e aplicaremos uma equação de momento e duas de força para encontrar . Começaremos com o momento em torno de D, pois ali existem duas forças desconhecidas que não aparecem no cálculo, então acharemos diretamente. Agora precisamos das coordenadas de , para calcularmos o momento de passando por . dista 0,9R da origem e OH está inclinado 15° com a horizontal, então:
Então as distâncias horizontal e vertical de para são:
As componentes vertical e horizontal de causam momento anti-horário no ponto dado por:
A distância horizontal entre e é:
Então o momento causado pela força em no ponto é:
Portanto:
Agora aplicamos os equilíbrios vertical e horizontal:
Substituindo os cossenos e o valor de :
Substituindo o valor de :