Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 53

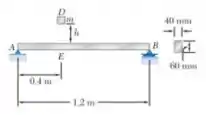
11.53 O bloco D de 10kg é solto desde uma altura h = 450 mm sobre uma viga de alumínio AB. Sabendo que E = 70 GPa, determine (a) a máxima deflexão do ponto E, (b) a máxima tensão na viga.

Passo 1

Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:

I = 1 12 40 60 3 = 720 × 10 3 m m 4 = 720 × 1 0 - 9 m 4

S = 1 6 40 60 3 = 24 × 10 3 m m 3 = 24 × 1 0 - 6 m 3

Apêndice D:

y m = P m a ² b ² 3 E I L

y m = P m ( 0,4 m ) ² ( 0,8 m ) ² 3 ( 70   G P a ) ( 720 × 1 0 - 9 ) ( 1,2   m )

Passo 2

(a)

y m = 0,5644 × 1 0 - 6 P m   o u   P m = 1,772 × 1 0 6 y m

U m = 1 2 P m y m = 1 2 1,772 × 1 0 6 y m y m = 885,9 × 1 0 3 y ² m

Trabalho de peso = W h + y m = m g h + y m  

( 10   k g ) ( 9.81 m / s ² ) ( 0.45   m + y m ) = 885,9 × 1 0 3 y ² m

885,9 × 1 0 3 y ² m - 98,1 y m - 44,145 = 0

Resolva quadrática:

y m = 7.114 × 1 0 - 3 m                         y m = 7,11 m m

Passo 3

(b)

P m = 1,772 × 1 0 6 y m = 1,772 × 1 0 6 ( 7.114 × 1 0 - 3 m )

P m = 12.61   k N

M m = M E = P m a b L = 12.61   k N ( 0,4   m ) ( 0,8   m ) 1,2 m

M m = 3.363   k N ∙ m

σ m = M m c I = M m S   3.363   k N ∙ m 24 × 1 0 - 6 m ³

σ m = 140,11 M P a

σ m = 140,1   M P a

Resposta

Então gurizada, como acabamos de calcular, temos a resposta de (a) y m = 7,11 m m e (b) σ m = 140,1   M P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel D de 35kg é abandonado do repouso na posição mostrada e é parando por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E=200 GPa para ambas as porções da haste, determ
O anel D de 15kg é abandonado do repouso na posição mostrada e é parando por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E=200 GPa para ambas as porções da haste, determ
O anel G de 48 kg é liberado do repouso na posição mostrada e é parado por uma placa conectada na extremidade em C da haste vertical ABC. Sabendo que E = 200 GPa para ambas as porções da haste, determ
O bloco C de 25 lb movendo-se horizontalmente com uma velocidade v 0 colide diretamente com a coluna AB conforme mostrado. Utilizando E = 29 × 10 6p s i , determine a maior velocidade v 0 para que a t
Resolva o problema 11.48 assumindo que a coluna AB seja rotacionada de 90° em relação ao seu eixo longitudinal.