Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 66
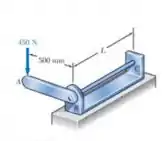
11.66 A barra de aço BC com 20mm de diâmetro está fixada na alavanca AB e engastada em C. A alavanca uniforme de aço tem 10mm de espessura e 30mm de largura. Usando o método do trabalho e da energia, determine o deslocamento do ponto A quando L = 600mm. Use E = 200 GPa e G = 77,2 GPa.
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
Membro AB. (Dobrando)
Passo 2
Membro BC. (Torção)
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Sabendo que as oito barras da treliça indeterminada mostradas nas figuras têm a mesma área de seção transversal, determine o esforço na barra A B .
Cada elemento da treliça mostrada é feito de aço e tem uma área de seção transversal de 400m m 2 . Usando E = 200G P a , determine a deflexão (o deslocamento) no ponto D causado pela carga de 16k N .
O navio em A começou a perfurar um poço de petróleo no fundo do oceano a uma profundidade de 1524m . A broca de perfuração de aço em forma de tubo tem um diâmetro externo de 203,2m m e uma espessura d
A haste A B é feita de aço para o qual a tensão de escoamento é σ E = 450M P a e E = 200G P a ; a haste B C é feita de uma liga de alumínio para a qual σ E = 280M P a e E = 73G P a . Determine a máxim
Um bloco de peso W é colocado em contato com uma viga em um certo ponto D e liberado. Mostre que a deflexão máxima resultante no ponto D é duas vezes maior do que a deflexão provocada por uma força es