Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 48
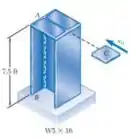
O bloco C de 25 lb movendo-se horizontalmente com uma velocidade colide diretamente com a coluna AB conforme mostrado. Utilizando determine a maior velocidade para que a tensão normal máxima na coluna não exceda 18 ksi.
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
Tensão máxima:
Momento máximo de flexão:
Força equivalente:
Passo 2
Do Apêndice D,
Passo 3
Energia cinética:
Equacionando,
Velocidade máxima.
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Cada barra de treliça mostrada na figura é feita de aço e têm seção transversal uniforme com área de 5i n 2 . Usando E = 29 × 10 6G P a , determine o deslocamento vertical do nó B provocado pela aplic
Cada elemento da treliça mostrada é feito de aço. A área da seção transversal do elemento B C é de 800m m 2 , e para todos os outros elementos a área é de 400m m 2 . Utilizando E = 200G P a , determin
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção trasnversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força P .
Usando E = 73,1G P a , determine de forma aproximada a máxima energia de deformação que a barra de alumínio acumulará se a tensão normal admissóivel é σ a d m = 151,7M P a .
Cada barra de treliça mostrada na figura tem uma seção transversal uniforme de área A . Usando o método do trabalho e da energia, determine o deslocamento horizontal do ponto de aplicação da força P .