Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 118
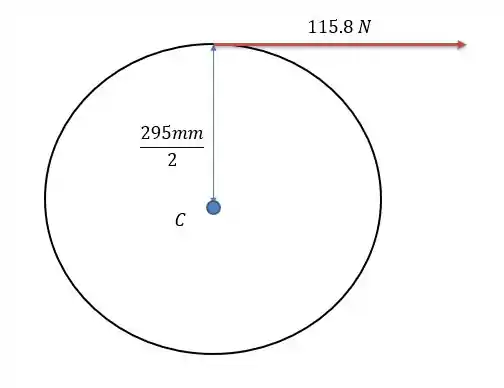
118- Um sistema automático de posicionamento de janelas para uma estufa está mostrado na figura. A janela tem uma massa de , com centro de massa em . Um motor (não mostrado) movimenta a engrenagem que, por sua vez, gira o trilho de posicionamento . Para a posição da janela mostrada, determine o torque do motor, que deve ser fornecido a roda dentada . Despreze o peso da barra .
Passo 1
Se separarmos a janela do sistema nós teremos o seguinte sistema de forças:
Da figura podemos tirar que vale , e com ele podemos rebater seus valores em e representados pelas retas vermelhas. Com eles podemos encontrar o valor de , pois o valor dos catetos e que formam o triângulo retângulo laranja serão de:
Logo o valor de será:
Passo 2
Agora precisamos encontrar o valor de imposto na janela.
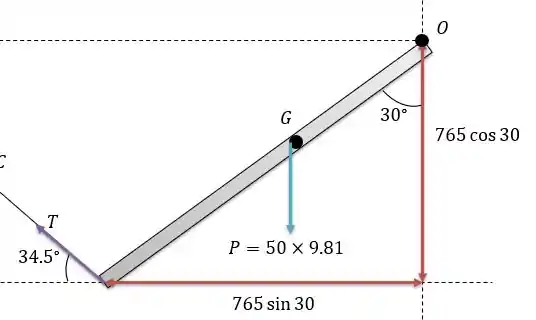
Para isso vamos fazer a somatória dos momentos em . E para isso precisamos saber rebater a barra e a força na vertical e na horizontal de maneira que ela tenha a seguinte forma equivalente:
Logo a somatória dos momentos em será:
Passo 3
A engrenagem de passo de pode ser aproximada para uma engrenagem de diâmetro , pois esse passo tem a ver com o passo diametral de uma engrenagem de dente reto. O que nos daria um sistema de forças equivalentes igual a:
