Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 89
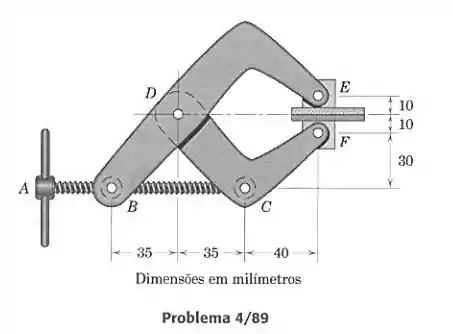
O grampo é ajustado de forma a exercer um par de forças compressivas de 200 N sobre as placas entre suas garras pivotadas. Determine a força no eixo rosqueado e o módulo da reação do pino em .
Passo 1
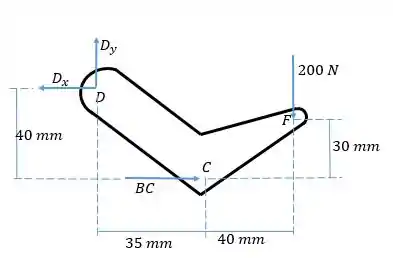
Aqui o primeiro passo é escolher qual ou quais corpos vamos isolar para fazer o diagrama de corpo livre e satisfazer as condições de equilíbrio. Se olharmos para a parte , vemos que nnela atuam a reação do pino em , a força do eixo aplicada em e a força de 200 N, para cima pela lei da ação e reação, aplicada em . Ou seja, esse corpo possui todas as forças que queremos encontrar. Vamos desenhar as forças que atuam sobre ele:
Passo 2
Para achar , podemos fazer o momento em torno de :
Se o eixo faz uma força para a esquerda em , o elemento faz no eixo uma força para a esquerda em , então é uma força de compressão.
Passo 3
Agora achamos e fazendo ser zero a soma das forças verticais e horizontais:
Então achamos o módulo da força: