Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 155
Um cabo pesando 40 newtons por metro de comprimento está suspenso do ponto A e passa pela pequena polia em B. Determine a massa m do cilindro preso ao cabo, que vai produzir uma deflexão de 10 m. Devido à pequena razão deflexão/vão, a aproximação de um cabo parabólico pode ser usada.
Passo 1
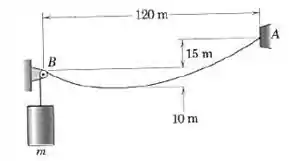
Primeiro vamos anotar as informações que a questão e a imagem nos oferecem, para facilitar a visualização:
O esquemático da questão segue abaixo:
Agora, vamos lembrar que a força trativa mínima no cabo é dada pela equação abaixo:
Como também lembre que a força trativa nos cabos é:
Note que, que a força trativa é igual tanto em A quando em B. Logo teremos 2 equações para acharmos .
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira:
Para A, teremos:
Para B, teremos:
Como,
Temos:
Resolvendo a equação vamos ter 2 soluções
Como x não pode ultrapassar 120, então:
Substituindo em qualquer equação da força trativa mínima temos:
Passo 3
Como já conhecemos a força trativa mínima agora é só substituir na equação que teremos a força trativa nos cabos. Logo,
Ou,
Logo em B teremos que,
Implica que,