Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 127
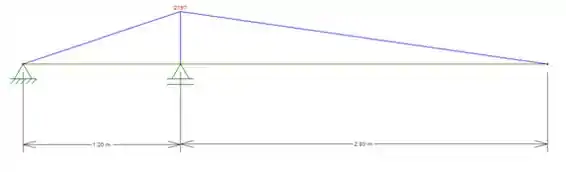
119- Desenhe os diagramas de cortante e de momento do trampolim, que sustenta o homem pesando 80 kg, preparado para mergulhar. Especifique o momento fletor de máximo módulo.
Passo 1
Considerando a gravidade igual a temos o peso do homem igual a:
Com esse valor podemos encontrar as reações em A e B, fazendo o seguinte sistema:
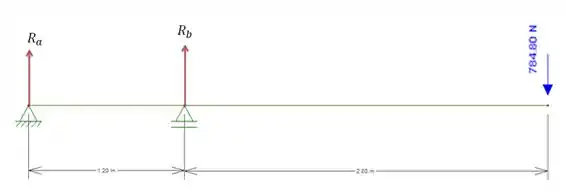
Fazendo a soma dos componentes verticais temos:
Agora fazendo a somatória dos momentos em A teremos (adotando o sentido horário como positivo):
Logo será:
Passo 2
Se fizermos o diagrama cortante teremos:
Passo 3
Pelo diagrama temos uma dica de que em B teremos o maior fletor, pois há uma maior variação da cortante, e fazendo pela direita teremos um momento de:
Resposta
Exercícios de Livros Relacionados
133- Sabe-se que resistência a flexão de uma viga com largura uniforme é proporcional ao quadrado da espessura y da viga. Para a viga em balanço mostrada. A espessura vale h , no apoio. Determine em f
136- Construa os diagramas de cortante e de momento para a viga carregada pelas cargas pontual e distribuída. Quais são os valores do cortante e do momento em x = 6 ? Determine o momento fletor máximo
126- Determine o cortante V e o momento M em uma seção 2m a direita da extremidade A da viga.
129- Desenhe os diagramas de cortante e de momento para a viga carregada e determine o módulo máximo M do momento fletor.
127- Desenhe os diagramas de cortante e de momento para a viga em balanço linearmente carregada, repetida aqui do Prob. 5/97. Determine o módulo máximo do momento fletor M .