Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 70

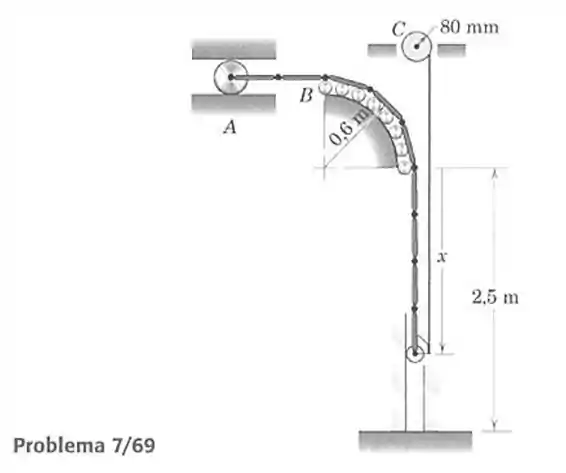
69- A figura mostra o projeto da seção transversal de uma porta industrial de 35   k g , com segmentos articulados, que passa sobre roletes posicionados sobre a guia cilíndrica. Quando a porta está fechada, a extremidade A está na posição B . Em cada lado da porta existe um cabo de controle, preso a extremidade inferior da porta e enrolado em um tambor C . Cada um dos dois tambores está ligado a uma mola de torção, que oferece uma resistência a torção que aumenta de 10 N m para cada revolução do tambor, começando a partir de uma posição não torcida da mola quando x = 0 . Determine o valor projetado de x para haver equilíbrio e prove que o equilíbrio nessa posição é estável.

Passo 1

O comprimento total da porta é de 2.5   m somado com um quarto de círculo de raio de 0.6   m o que dá um valor de:

L = 2.5 + 0.6 π 2 = 3.44   m

E como a porta pesa 35   k g nós temos uma densidade linear igual a:

ρ = 35 3.44 = 10.17 k g m

Logo a massa da porta vai alterando a medida que ela vai descendo a porta, pois ela vai ganhando corpo a media que vai se afastando da reta de energia potencial nula.

Logo:

m = 10.17 x

Isso será importante para saber a variação da energia potencial gravitacional do sistema, pois traçando a linha de energia nula passando pelo ponto A temos:

V e = - 10.17 x × 9.81 × 0.6 + x 2

Onde a porta já começa separada de 0.6   m devido a posição nos roletes e x / 2 é a mudança do centro de gravidade em relação ao ponto nulo.

Ainda vamos considerar um acréscimo V c referente a energia potencial do tambor C que não muda de lugar durante todo o trajeto fazendo com que a energia potencial do sistema todo seja.

V e = V c - 99.77 0.6 + x 2

Passo 2

Para a energia potencial elástica temos que levar em consideração que temos dois tambores que produzem uma energia potencial elástica torcional, logo a energia será de:

V e = 2 1 2 K t θ 2 = K t θ 2

Como foi dito que os tambores oferecem uma resistência de 10   N m para cada 2 π   r a d então temos uma resistência torcional igual a:

K t = 10 2 π

Logo a energia potencial elástica será:

V e = 10 2 π θ 2

Porém θ varia de acordo com a rotação do tambor C de modo que:

x = 80 × 10 - 3 × θ

θ = x 0.08

Logo:

V e = 5 π × x 0.08 2 = 248.68 x 2

Logo a energia total do sistema será:

V = 248.68 x 2 + V c - 99.77 0.6 x + x 2 2

Passo 3

Fazendo a primeira derivada em relação a x temos:

d V d x = 497.36 x + 0 - 99.7 × 0.6 - 99.7 x

d V d x = 397.66 x - 59.82

O que nos dá uma posição de equilíbrio em:

d V d x = 0

x = 59.82 397.66 = 0.15   m

E a segunda derivada nos mostra que:

d 2 V d x 2 = 397.66 → p o s i t i v o

Que a posição encontrada e o sistema é estável.

Acreditamos que houve erro de digitação e o peso que eles queriam colocar é de 135   k g .

Resposta

x = 0 . 15   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A janela de atendimento em um restaurante consiste em portas de vidro acionadas automaticamente por um motor que fornece um torque M a cada porta. As extremidades, A e B , se movem ao longo das guias
Quando θ = 30 ° , o bloco uniforme de 25k g comprime as duas molas horizontais em 100m m . Determine a intensidade dos momentos de binário aplicados M necessários para manter o equilíbrio. Considere k
O elemento esbelto de peso W se apoia na parede e no piso lisos. Determine a intensidade da força P necessária para mantê-lo em equilíbrio para determinado ângulo θ .
O “pantógrafo de Nuremberg” está sujeito a uma força horizontal P=600N . Determine a rigidez k da mola para o equilíbrio quando θ = 60 ° . A mola não está esticada quando θ = 15 ° .
Uma mesa de servir uniforme de 5k g está apoiada em cada lado por um par de membros idênticos, A B e C D , e molas C E . Se a tigela tem massa de 1k g , determine o ângulo u quando a mesa está em equi