Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 129

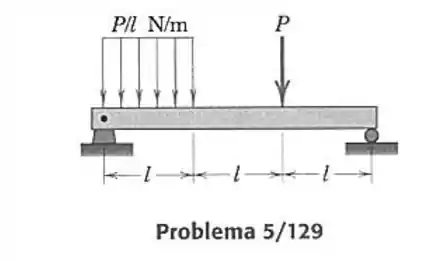
129- Desenhe os diagramas de cortante e de momento para a viga carregada e determine o módulo máximo M do momento fletor.

Passo 1

Como a carga distribuída é retangular ela contribui na viga uma força resultante P na posição de l / 2 deixando nossa viga da seguinte forma.

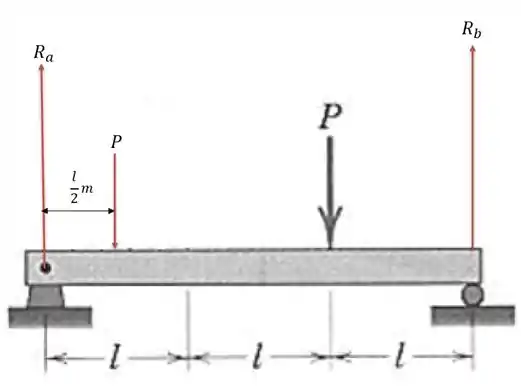
Chamando a reação vertical no suporte esquerdo de R a e a da direita de R b nós teremos a somatória das forças verticais será igual a:

R a + R b = 2 P

Agora fazendo a somatória dos momentos em A igual a zero e adotando o sentido horário como positivo nós teremos:

P l 2 + 2 P l - 3 l R b = 0

R b = 5 P 6

Logo R a será:

R a = 2 P - 5 P 6 = 7 P 6

Passo 2

Agora que encontramos as reações podemos analisar setor a setor nossa viga:

Para 0 < x < l :

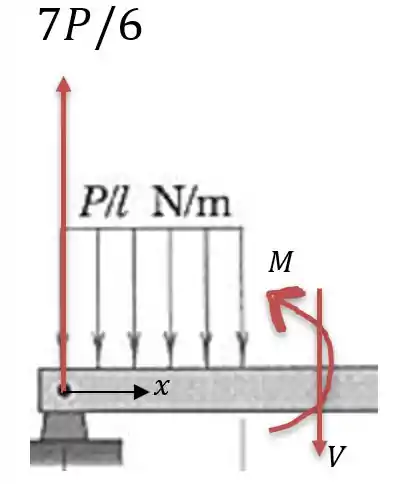
Nessa posição o valor da cortante será:

V = 7 P 6 - P l x

Integrando a cortante temos o momento:

M = 7 P 6 x - P x 2 2 l

Para x = l a cortante vale P / 6 e o momento fletor vale 2 P l / 3   .

Para l < x < 2 l :

Nesse intervalo não existe nenhuma força somente existe as forças e os momentos resultantes na seção anterior. Logo a cortante nessa seção será:

V = P 6

E o momento fletor:

M = 7 6 P x - P l ( x - l 2 )

Para 2 l < x < 3 l :

Nessa seção temos a existência da força P no começo, logo nossa cortante será:

V = P 6 - P = - 5 P 6

E o momento fletor:

M = 7 6 P x - P l x - l 2 - P ( x - 2 l )

Podemos também fazer pelo outro lado que ficaria mais fácil.

M = R B x = 5 P 6 x

Que é o momento da vindo da seção anterior multiplicado pela cortante atual multiplicado pela distância medida a partir dessa nova origem.

Passo 3

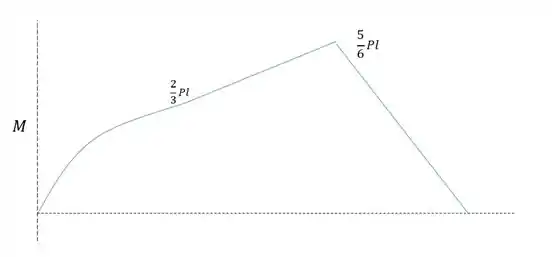
Diagrama da cortante:

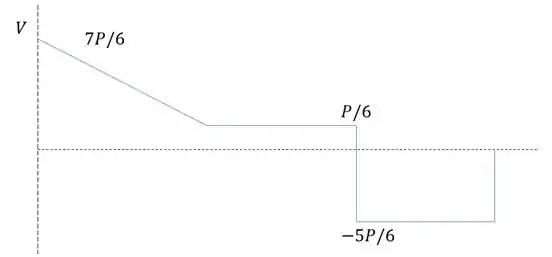
Diagrama do momento fletor:

Resposta

M max ⁡   = 5 6 P l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as componentes x , y e z da carga interna no ponto C da tubulação. Despreze o peso da tubulação. Faça F 1 = - 24 i - 10 kk N , F 2 = - 80 ik N e M = - 30 kk N ∙ m .
A lança do guindaste suporta uma carga de 3,75k N através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto D da lança quando o carri
O macaco A B é usado para acertar a viga fletida D E usando a montagem mostrada. Se a força compressiva axial no macaco é de 25k N , determine o momento interno desenvolvido no ponto C da viga superio
Determine as componentes x , y e z da carga interna em uma seção passando pelo ponto C na tubulação. Despreze o peso da tubulação. Faça F 1 = 350 j - 40 0 kk N e F 2 = 15 0 i - 300 kk N .
Determine a força normal interna, o esforço cortante e o momento nos pontos F e G da viga composta. O ponto F está localizado à direita da força 2,5k N , enquanto o ponto G está localizado à direita d