Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 121
121- Cada uma das estruturas mostradas nas figuras consiste em dois elementos em forma de ligados por duas hastes rígidas. Para cada estrutura, determine as reações nos apoios e indique se a estrutura é rígida.
Passo 1
Fazendo o diagrama de forças para a letra nós temos:
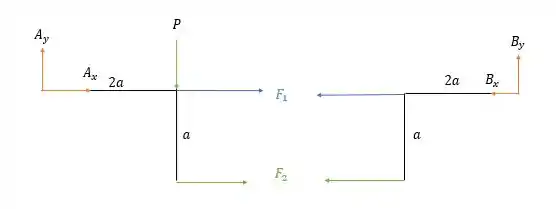
Fazendo a somatória dos momentos em na estrutura a esquerda nós temos:
Pela somatória das forças verticais na estrutura da esquerda teremos:
E pela somatória das forças horizontais:
Agora vamos para a estrutura a direita dos cabos.
A soma das forças verticais nos dá:
E a somatória dos momentos em nos dá:
Porém pera. Nós encontramos:
Isso daria
Isso nos diz que a estrutura não é rígida, pois tem que ser diferente de zero.
Passo 2
Note que na letra o apoio em é de um grau somente. Nos dando o seguinte diagrama de forças.
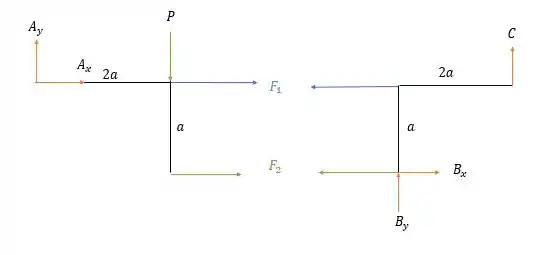
Fazendo a somatória dos momentos em na estrutura a esquerda dos cabos nós teremos:
E fazendo então a somatória das forças verticais nós teremos:
E a somatória das forças horizontais:
Agora para a estrutura a direita dos cabos teremos a seguinte somatória dos momentos em .
E a somatória das forças horizontais nos dá:
Isso nos diz que
E que pela soma das forças verticais temos:
E a somatória dos momentos em nos dá:
Logo:
Logo não existe nenhum impeditivo dessa estrutura não ser rígida, isso é, não tem nada que force
Passo 3
Agora as forças para a letra .
Fazendo a somatória dos momentos em na estrutura a direita dos cabos nós temos:
O que é:
Agora fazendo a somatória dos momentos em na estrutura a esquerda dos cabos nós temos:
Substituindo o valor de temos:
Logo:
Dessa forma pela soma das forças horizontais nas duas estruturas nós iremos ter:
E pela soma das forças verticais:
Precisa nem dizer que é uma estrutura rígida.