Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 168

Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuando no elemento A B C .

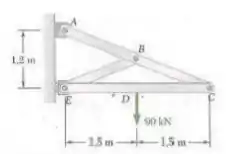
Passo 1

Para toda nossa estrutura podemos aplicar as condições de equilíbrio de tal forma que consigamos encontrar as forças que atuam no elemento desejado pelo problema. Sendo assim, teremos

∑ M e = 0 → - A x ⋅ 1,2 - 90 k N ⋅ 1.5 = 0 → A x = - 112.5   k N   e s t á   p a r a   a   e s q u e r d a  

∑ F y = 0 → A y - 90 k N = 0 → A y = 90 k N

Passo 2

A partir da geometria do problema podemos deduzir que

B y = 0.6 1.5 ⋅ B x → B y = 2 5 ⋅ B x

Aplicando as condições de equilíbrio para o membro A B C temos

∑ M c = 0 → 112.5 k N ⋅ 1.2 m - 90 k N ⋅ 3 m - B x ⋅ 0.6 m - B y ⋅ 1.5 m = 0

112.5 k N ⋅ 1.2 m - 90 k N ⋅ 3 m - B x ⋅ 0.6 m - 2 5 ⋅ B x ⋅ 1.5 m = 0

112.5 k N ⋅ 1.2 m - 90 k N ⋅ 3 m - 5 B x 5 ⋅ 0.6 m - 2 5 ⋅ B x ⋅ 1.5 m = 0

112.5 k N ⋅ 1.2 m - 90 k N ⋅ 3 m - 6 B x 5 = 0 → B x = - 112.5 k N   p r a   e s q u e r d a

B y = 2 5 ⋅ 112.5 k N = - 45 k N   p r a   b a i x o

Por fim, teremos

∑ F x = 0 → C x - 112.5 k N - 112.5 k N = 0 → C x = 225   k N

∑ F y = 0 → C y + 90 k N + 45 k N = 0 → C y = - 1 35 k N   ( p r a   b a i x o )

Pronto, já temos tudo que o enunciado desejava de nós.

Resposta

A x = 112.5 k N   ,   A y = 90 k N , B x = 112.5 k N   , B y = 45 k N ,   C x = 225   k N   e   C y =   135 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a maior força P que pode ser aplicada à treliça de modo que nenhum dos membros esteja sujeito a uma força maior que 2,5k N em tração ou 2k N em compressão.
A treliça é fabricada usando membros que têm um peso de 0,2k N / m . Remova as forças externas da treliça e determine a força em cada membro devido ao peso dos membros. Indique se os membros estão sob
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. O bloco possui uma massa de 40k g .
54. A treliça espacial suporta uma força F → = - 500 i + 600 j + 400 kN . Determine a força em cada membro e indique se os membros estão sob tração ou compressão.
6.24. Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão. Faça P = 4k N .