Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 121
121- Determine a força atuando no elemento na conexão para o suporte espacial carregado mostrado. Cada conexão pode ser tratada como uma rótula.
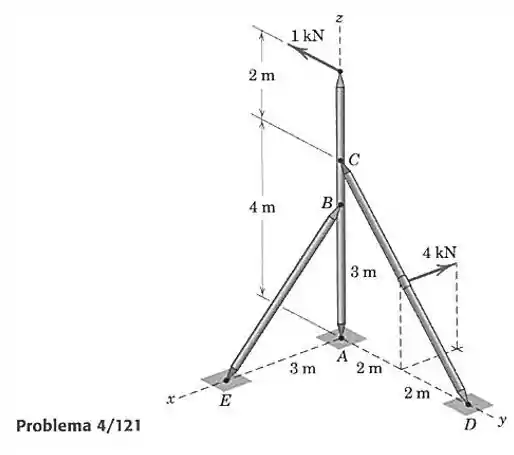
Passo 1
Vamos separar os elementos de modo que consigamos visualizar as forças atuando em todos os elementos de maneira correta.
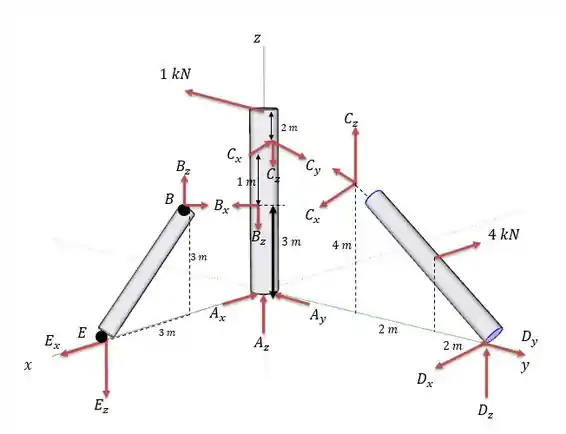
Assim como para uma direção a somatória de momentos em qualquer eixo em um corpo qualquer tem que ser zero. Além de que não iremos ter forças em no elemento uma vez que não iremos ter nenhum momento sendo aplicado nessa região , mas isso pode ser descoberto depois sem problemas. Além de que se quisermos inverter o sentido dos vetores no desenho também não iremos ter maiores problemas, só encontraremos forças negativas depois.
Além de lembrar dos cálculos de momento nos eixos .
Passo 2
No corpo se fizermos a multiplicação da força na distância nós teremos um momento para anular precisaremos da força , logo:
Com essa força encontrada posso olhar para o corpo e encontrar a força ao fazer o somatório dos momentos em no eixo , já que o eixo encontra-se em .
Ainda observando para o corpo temos que se fizermos a somatória das forças horizontais temos que:
Passo 3
Agora vamos fazer a somatória de momentos utilizando a força de que aponta na direção j no eixo k no ponto . Isso é a somatória dos momentos em .
Agora fazendo a somatória das forças em nesse elemento ser zero nós iremos ter:
Passo 4
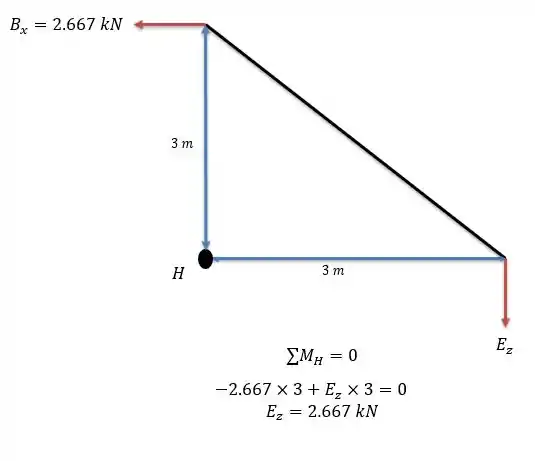
Pelo valor de encontrado no fim do passo nós conseguimos pela somatória de momentos na base do triângulo retângulo encontrar que (pode ser melhor visto na figura de apoio no final desse passo):
Até por conta dos catetos serem iguais, então por conta disso descobrimos que:
O mesmo raciocínio vale para .
Logo:
Logo fazendo a somatória das forças em no elemento temos que:
Passo 5
Podemos fazer agora o módulo da reação já que temos as três componentes dessa reação.
Resposta
A união desses três elementos cria as meninas superpoderooo... nos dá o módulo de :