Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 40
O encanamento está sujeito à força de F = {600i + 800j - 500k} N. Determine o momento dessa força em relação ao ponto B.
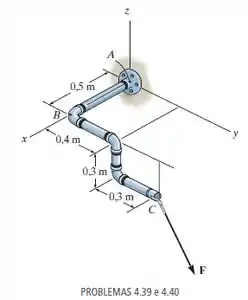
Fonte: Estática Mecânica para Engenharia – 14ª ed
Passo 1
Fala aí, estamos pegando o jeito?!
Bora lá!!
Bem, o problema quer o momento da força F em relação ao ponto B agora. E, para nossa alegria continuar, a força F já está em coordenadas cartesianas!!
O que isso nos sugere?
Isso mesmo, que apliquemos a eq. 4.7 do livro texto, a equação do momento de uma força em relação a um ponto:
Passo 2
Mas primeiro vamos encontrar o vetor posição :
Assim, aplicando a equação 1:
Assim, aplicando o determinante, temos:
Então
Resposta
Portanto:
Exercícios de Livros Relacionados
O encanamento esta sujeito á força de 80N . Determine o momento dessa força em relação ao ponto B .
47. A força F → = 6 i + 8 j + 10 kN cria um momento em relação ao ponto O de M 0 = - 14 i + 8 j + 2 kN ⋅ m . Se a força passa por um ponto tendo uma coordenada x de 1m , determine as coordenadas y e z
53. A ferramenta é usada para fechar válvulas de gás que são difíceis de acessar. Se a força F → é aplicada no cabo, determine a componente do momento criada em relação ao eixo z da válvula.
60. Determine a intensidade do momento produzido pela força F = 200N em relação ao eixo da dobradiça (o eixo x) da porta.
55. Determine o momento da força F → em relação ao eixo que se estende entre A e C. Expresse o resultado como um vetor cartesiano.