Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 122
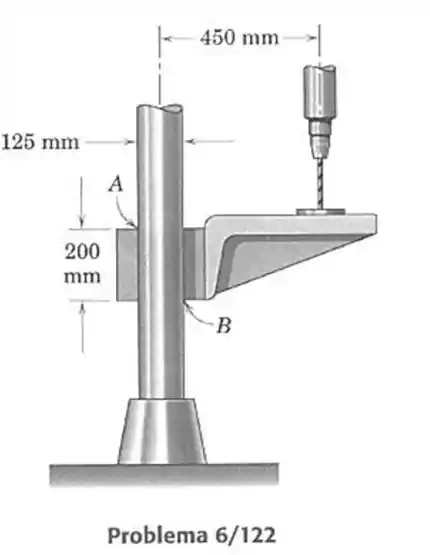
122- O coeficiente de atrito estático entre a braçadeira da furadeira de bancada e a coluna vertical vale . Se o operador esquecer-se de prender a trava, a braçadeira e a mesa deslizarão para baixo da coluna sob a ação da pressão da furadeira, ou o atrito será suficiente para mantê-las no lugar? Despreze o peso da mesa e da braçadeira comparado com a pressão da furadeira e assuma que ocorre contato nos pontos e .
Passo 1
Vamos considerar que existe a força de ação da furadeira e que coluna vertical reage a essa força com o ângulo de atrito formado entre os pontos de contato com a braçadeira respeitando o ângulo de atrito entre elas, tal como pode ser vista no desenho abaixo.
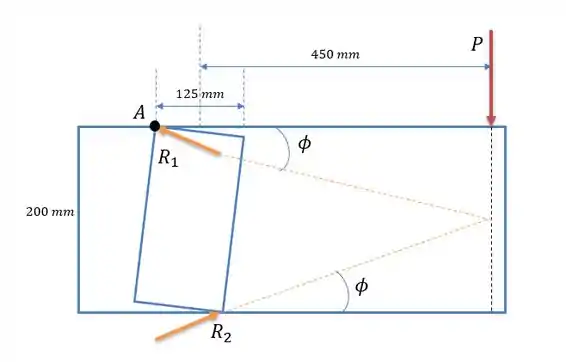
Considerando que a barra tende a rotacionar no sentido horário, logo as reações que surgem no sentido anti-horário porém com uma angulação que valerá:
Porém não vamos utilizar essa angulação, vamos utilizar a somatória das forças e dos momentos e se acharmos uma angulação maior no sistema de forças representado na figura acima então a furadeira escorrega, se for menor, ela satisfaz.
Passo 2
Fazendo a somatória das forças horizontais tranquilamente encontramos:
Para a somatória das forças verticais temos:
Agora a somatória dos momentos em :
Como :
Substituindo o valor de encontrado na equação 1:
Dividindo:
Como o coeficiente de atrito limite deu menor que o coeficiente de atrito dado na questão, logo a coluna segura a furadeira.
Resposta
O atrito entre a braçadeira e a coluna segura a furadeira.