Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 106

A vertical consiste em uma estrutura, três tambores fixos de diâmetro 8   p o l e seis pequenas rodas-guia com um peso combinado de 50   l b . Determine o peso mínimo W necessário para manter o carrinho em equilíbrio para qualquer posição em suas guias verticais. O coeficiente de atrito entre o cabo de luz e o tambor é 0,30 .

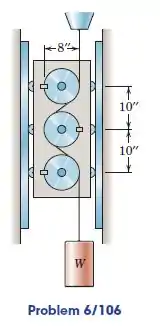
Passo 1

Queremos o peso mínimo W necessário para manter o carrinho em equilíbrio para qualquer posição em suas guias verticais.

Precisamos saber o ângulo de contato entre o ponto de contato e o cilindro superior.

γ = cos - 1 ⁡ 8 / 2 10 / 2

γ = 36,87 °

O ângulo de contato entre o cabo e o tambor superior será:

α = 90 ° - γ

α = 53,13 °

E finalmente, o ângulo de contato total é dado por:

β = 4 α

β = 4 53,13 ° π 180 °

β = 3,709   r a d

Passo 2

O coeficiente mínimo de atrito entre o cabo e o eixo é dado por:

ln ⁡ T 2 T 1 = μ β

Ou:

T 2 T 1 = e μ β

Onde T 1 é a tensão na corda no lado tenso e T 2 no lado frouxo.

Substituindo os respectivos valores, temos que:

T W = e 0,3 3,709

T = 3,0426 W

Passo 3

Vamos aplicar a análise do equilíbrio vertical:

∑ F y = 0

T - 50   l b - W = 0

3,0426 W - 50 - W = 0

2,0426 W = 50

W = 24,5   l b

Este é o valor de W necessário para manter o sistema em equilíbrio para qualquer posição em suas guias verticais.

Temos que:

P = m g 6

Logo:

ln ⁡ m g m g 6 = μ β

ln ⁡ 6 = μ 5 π 2

Resolvendo, temos que:

μ = 1,791 5 π 2

μ = 0,228

Resposta

μ = 0,228

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A empilhadeira tem peso de 12 kN e centro de gravidade em G. Se as rodas traseiras são tracionadas, enquanto as dianteiras estão livres para rodar, determine o número máximo de caixas de 150 kg que a
Determine o ângulo ϕ no qual a força aplicada P deverá atuar sobre o tubo de modo que a intensidade de P seja a menor possível para puxá-lo rampa acima. Qual é o valor correspondente de P ? O tubo pes
O tubo com peso W deve ser puxado para cima no plano indicado com inclinação α usando uma força P . Se P age em um ângulo ϕ , mostre que, para deslizar, P = W sen ⁡ α + θ / cos ⁡ ϕ - θ , onde θ é o ân
O automóvel tem massa de 2Mg e centro de massa em G . Determine a força de reboque F exigida para mover o carro se os freios traseiros estão acionados e as rodas dianteiras estão livres para rodar. Co
A força P de 85l b é aplicada à caixa de 200l b , que fica estacionária antes de a força ser aplicada. Determine a magnitude e a direção da força de atrito F exercida pela superfície horizontal na cai