Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 154
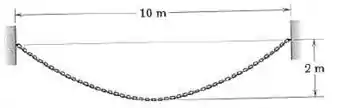
Ache o comprimento total L da corrente que terá uma deflexão de 2 m quando for suspensa de dois pontos, distando de 10 m e situados sobre a mesma linha horizontal.
Passo 1
Primeiro vamos anotar as informações que a questão e a imagem nos oferecem, para facilitar a visualização:
A figura abaixo representa o esquemático da questão:
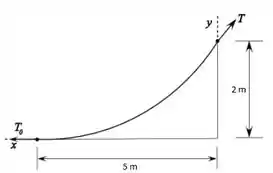
Agora, vamos lembrar a equação da curva formada pelo cabo abaixo:
Como também, é de conhecimento a equação que relaciona o comprimento s:
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira, temos:
Resolvendo a equação acima, teremos que:
Passo 3
Agora basta utilizarmos a equação que descreve o comprimento s que teremos nossa resposta, mas cuidado. Note que,
Logo,
Substituindo os valores, temos:
Resposta
Exercícios de Livros Relacionados
Desenvolva uma expressão para a projeção F D C da força F → sobre a linha direcionada de D a C .
Determine o ângulo θ entre a força de 200N e a linha O C .
Se M está no centro da face A B C D do sólido retangular, expresse F como um vetor em termos dos vetores unitários i , j e k . Determine a projeção escalar de F ao longo da linha A E . Os valores de F
Uma força F é aplicada à superfície da esfera como mostrado. Os ângulos θ e ϕ localizam o ponto P e M é o ponto médio de O N . Expresse F em forma vetorial, usando as coordenadas x , y e z dadas.
A porta de acesso é mantida na posição aberta a 30 ° por uma corrente A B . Se a força trativa na corrente é de 100N , determine a projeção desta força sobre o eixo diagonal C D da porta.