Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 142

Um macaco tipo tesoura com um único fio quadrado que engata o colar roscado G e transforma em um rolamento axial de esferas em D está sendo projetado. A rosca deve ter um diâmetro médio de 10   m m e um avanço (avanço por rotação) de   3   m m . Com um coeficiente de fricção de 0,20 para as roscas engraxadas, (a) calcular o torque M no parafuso necessário para levantar uma carga de 1000   k g a partir da posição mostrada e (b) calcular o torque M necessário para abaixar o carregar da mesma posição. Suponha que a plataforma A B e a linha D G permanecerão horizontais sob carga. Despreze o atrito no rolamento em D .

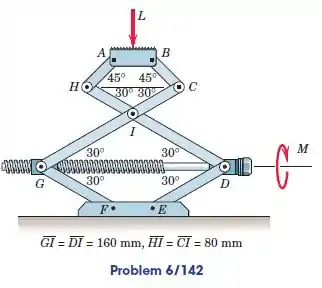
Passo 1

Precisamos de uma expressão para T que represente a subida e a descida da caixa.

O coeficiente mínimo de atrito entre o cabo e a polia é dado por:

ln ⁡ T 2 T 1 = μ β

Ou:

T 2 T 1 = e μ β

Onde T 1 é a tensão na corda no lado tenso e T 2 no lado frouxo.

Substituindo os respectivos valores, temos que:

T T 1 = e μ β

T 1 = T e - μ β

Passo 2

Para levantar o peso, temos que a condição de trabalho deve ser:

T sen ⁡ θ + T 1 sen ⁡ θ = m g

Substituindo os dados, temos que:

T sen ⁡ θ + T e - μ β sen ⁡ θ = m g

T = m g sen ⁡ θ 1 + e - μ β

Passo 3

No momento da descida, a ordem das tensões é invertida, e T representa o lado frouxo, logo:

T 1 T = e μ β

Realizando o mesmo procedimento do passo anterior, temos que:

T sen ⁡ θ - T 1 sen ⁡ θ = m g

Substituindo os dados, temos que:

T sen ⁡ θ - T e μ β sen ⁡ θ = m g

T = m g sen ⁡ θ 1 - e μ β

Resposta

  1. T = m g sen ⁡ θ 1 + e - μ β

  2. T = m g sen ⁡ θ 1 - e μ β
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O freio manual é usado para impedir o giro da roda quando ela estiver sujeita a um momento de binário M 0=360N m . Se o coeficiente de atrito estático entre a roda e o bloco em B é u=0,6 , determine a
Determine a intensidade da força P necessária para iniciar o reboque da caixa de 40k g . Considere u=0,3 .
A viga é apoiada por um pino em A e um rolete em B , que possui peso desprezível e raio de 15m m . Se o coeficiente de atrito estático é u B = u c = 0,3 , determine o maior ângulo θ da inclinação de m
O freio manual consiste em uma alavanca conectada por um pino e um bloco de atrito em B . O coeficiente de atrito estático entre a roda e a alavanca é μ s = 0,3 , e um torque de 5N ⋅ m é aplicado à ro
O automóvel tem massa de 2M g e centro de massa em G . Determine a força de reboque F exigida para mover o carro. Os freios dianteiros e traseiros estão acionados. Considere μ s = 0,3 .