Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 117

Resolva o Problema 8.116 , supondo que o tambor B esteja fixo e não possa girar.

Passo 1

Bom galera, começamos fazendo um diagraminha:

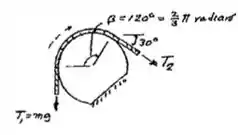
Com isso temos:

T 1 = m g

β = 120 ° = 2 3 π   r a d i a n o s

T 2 T 1 = T 2 m g = e μ 2 3 π

→ T 2 = m g e 2 μ π 3

Passo 2

Show de bola, vamos descobrir qual o menor m para o bloco C continuar em repouso. Pra isso a gente usar a equação que encontramos no passo 1 :

T 2 = m g e 2 μ π 3

→ T 2 = m g e 2 0 , 3 5 π 3

→ T 2 = 2,0814 m g

Agora, usamos a equação de repouso para o bloco C :

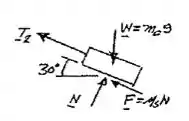
Paralela a N :

∑ F = 0

→ N - m c ⋅ g ⋅ cos ⁡ 30 °

→ N = m c ⋅ g ⋅ cos ⁡ 30 °

E F pode ser dado assim:

F = μ s N

→ F = μ s ⋅ m c ⋅ g ⋅ cos ⁡ 30 °

→ F = 0,35 ⋅ m c ⋅ g ⋅ cos ⁡ 30 °

→ m c = 100   k g

Passo 3

Também usamos a equação de equilíbrio no eixo perpendicular à N :

∑ F = 0

→ T 2 + F - m c   g cos ⁡ 30 ° = 0

→ 2,0814 m g + 0,35 m c   g cos ⁡ 30 ° - m c   g sin ⁡ 30 ° = 0

→ 2,0814 m = 0,19689 m c

→ 2,0814 m = 0,19689 100

→ m = 9,46   k g

Passo 4

Então, calculamos o menor m para começar o movimento. Usamos a equação:

T 2 T 1 = e μ s β

→ m g T 1 = e 0,35 2 3 π

→ T 1 = m g 2,0814 = 0,48045 m g

Agora, a equação de equilíbrio:

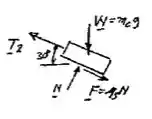
Paralelo a N :

∑ F = 0

→ N - m g cos ⁡ 30 ° = 0

→ N = m g cos ⁡ 30 °

Então F fica:

F = μ s N

→ F = 0,35 m c g cos ⁡ 30 °

E na perpendicular á N :

∑ F = 0

→ T 2 - F - m c g sin ⁡ 30 ° = 0

→ 0,48045 m g - 0,35 m c g cos ⁡ 30 ° - m c g 0,5 = 0

→ 0,48045 m = 0 , 80311 m c

→ 0,48045 m = 0 , 80311 ( 100 )

→ m = 167,2   k g

Passo 5

Por fim, usamos a equação de equilibrio para que ela continue a se mover plano acima a uma velocidade constante. Assim, encotraremos:

m = 121   k g

Resposta

(a)

m = 9,46   k g

(b)

m = 167,2   k g

(c)

m = 121   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o valor mínimo de θ para o qual o equilíbrio é possível se (a) μ s A = 0.60 e μ s B = 0.20 e (b) μ s A = 0.40 e μ 8 B = 0.10 .
As extremidades da braçadeira de tubo são projetadas para caber em 1/2 pol. Padrão. tubo de água de aço (diâmetro externo = 0,840 pol.). A conexão direita desliza livremente ao longo do tubo quando a
Uma mangueira de jardim com uma massa de 1,2 kg / m está em total contato com o solo de B a C. Qual é o componente horizontal Px da força que o jardineiro deve exercer para puxar a mangueira ao redor
O cirurgião arborícola de 180 libras se abaixa com a corda sobre um galho horizontal da árvore. Se o coeficiente de fricção entre a corda e o membro for 0,60, calcule a força que o homem deve exercer
Calcule a força horizontal P necessária para elevar a carga de 100 kg. O coeficiente de atrito entre o cabo e as barras fixas é de 0,40.