Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 128
128- Desenhe os diagramas de cortante e de momento para a viga mostrada. Determine a distância b, medida a partir da extremidade esquerda, ao ponto entre os suportes onde o momento fletor é nulo.
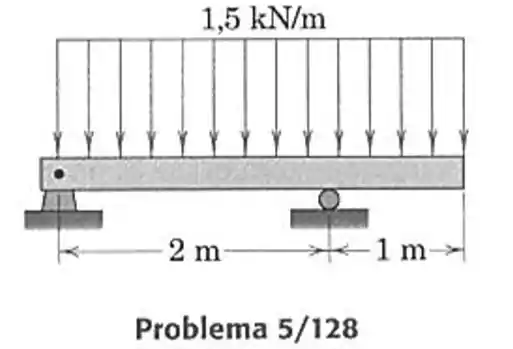
Passo 1
Antes de calcular as forças nos apoios primeiramente vamos descobrir qual a contribuição total dessa carga, e onde ela se situa.
O que nos abre a possibilidade de redesenhar a carga da seguinte forma:
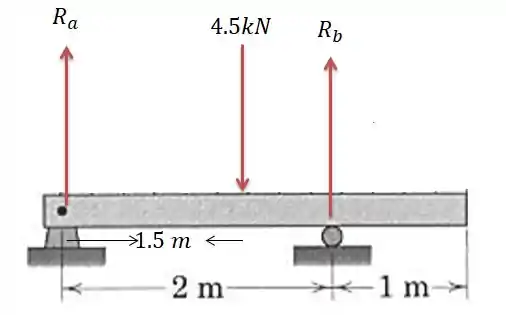
Passo 2
Pelo somatório das forças nós encontramos:
E pelos momentos em A:
Logo será:
Passo 3
Com essa reações conseguimos plotar o diagrama da cortante:
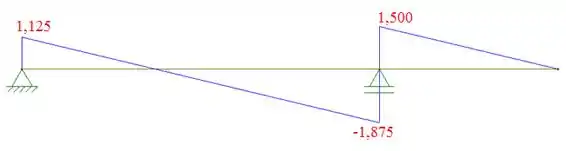
O que nos dá uma equação de cortante de 0 até 2m de e de 2m até 3m, uma equação de cortante de
Passo 4
E o diagrama de momento fletor igual a:
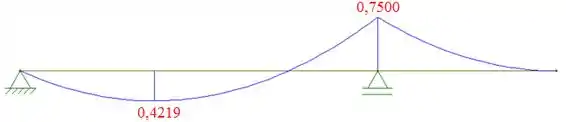
Para sabermos a equação do momento fletor de a basta integrarmos a equação da cortante:
Essa equação será zero em e: