Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 38
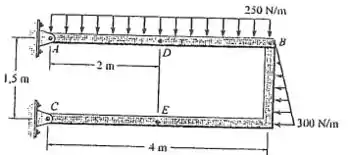
Determine a força normal interna, o esforço cortante e o momento no ponto da estrutura com dois membros.
Passo 1
Fala, querido!
Ele pede os esforços internos em Para resolver esse tipo de questão tem um passo a passo. Só seguir que dá bom:
- Fazer DCL
- Achar reações nos apoios necessárias
- seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
E o que é legal é que essa análise é feita com as queridinhas equações de equilíbrio.
Vamos entender essa estrutura. Ela é formada por essa barra horizontal e o membro . Esse dois se ligam por um pino.
Uma forma de resolver essa estrutura (achar as reações) é olhar cada membro e suas reações. É isso que vamos fazer.
Vamos começar achando as reações do membro em , isso porque só precisamos saber dessas reações para analisar o membro , onde nossa seção está. Bora!
Passo 2
Então, primeiramente pode-se fazer o DCL da seção para conseguir determinar uma das reações de tal que:
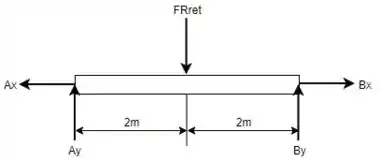
Repara que como ali em é um pino, só temos essas duas reações.
Deve-se lembrar que o carregamento retangular gera uma força resultante dada por:
E a posição do seu centroide é dada por:
Com isso, supondo que o momento é positivo no sentido horário, pode-se fazer o somatório de momentos em relação ao ponto e obter:
Passo 3
Olhando para a estrutura de forma geral, a gente vê que as reações horizontais em são influenciadas pelo carregamento em .
Agora, fazendo o DCL da seção para conseguir determinar a reação horizontal de tem-se que:
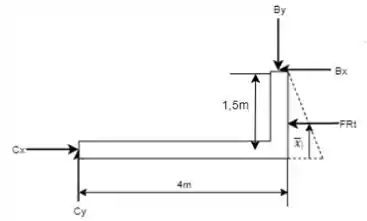
Deve-se lembrar que o carregamento triangular gera uma força resultante dada por:
E a posição do seu centroide é dada por:
Com isso, supondo que o momento é positivo no sentido horário, pode-se fazer o momento em relação ao ponto e obter:
Passo 4
Agora repara, a gente já conhece as reações em uma ponta do membro , então a gente já pode secionar ele em e olhar só para a parte onde sabemos as reações, e achar os esforços internos em .
Enfim, com as reações em determinadas é possível fazer o DCL da seção e encontrar os resultados desejados. Portanto:
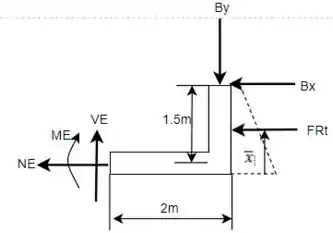
Com isso, é possível montar as equações de equilíbrio.
Tem-se, então, para o eixo :
O sinal negativo indica que a força normal age no sentido oposto, ou seja, age para a direita.
Para o eixo será dado por:
E, por fim, fazendo o momento em relação ao ponto de referência e supondo novamente que o momento é positivo no sentido anti-horário: