Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 9
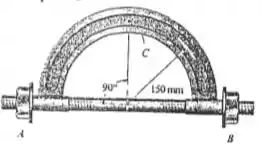
A barra parafusada está sujeita a uma tração de . Determine a força normal interna, o esforço cortante e o momento no ponto .
Passo 1
Para determinar o que se pede, deve-se fazer o diagrama de corpo livre da viga para que seja possível determinar alguma reação externa ao apoio da viga. Após isso, deve-se seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
Como neste caso o corpo não está apoiado sobre um suporte, é possível fazer o diagrama de corpo livre da barra já seccionada no ponto de interesse diretamente e aplicar as equações de equilíbrio.
Passo 2
Então, o DCL da barra seccionada em é dada por:
Então, aplicando as equações de equilíbrio obtém-se para o eixo :
Para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo:
Os sinais negativos indicam a oposição dos sentidos adotados. Logo, a força normal atua para cima e o momento atua no sentido horário.