Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 49

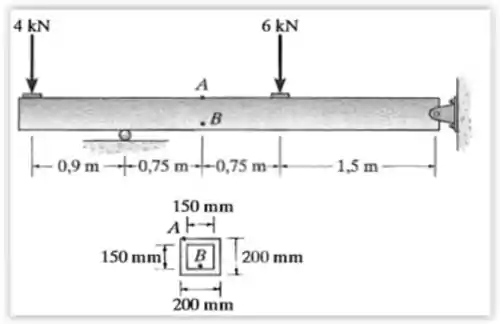
49. A viga-caixão está sujeita às cargas mostradas na figura. Determine as tensões principais na viga no ponto A e no ponto B .

Passo 1

Vamos primeiro, montar os diagramas de corpo livre da viga:

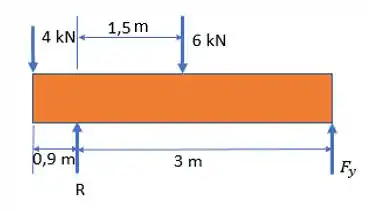
E depois realizar o somatório de momentos em relação ao ponto R e das forças verticais, considerando o eixo y positivo:

↶ + ∑ M = 0

4   k N × 0,9   m - 6   k N × 1,5   m   + F y × 3   m   = 0  

F y = 4   k N × 0,9   m - 6   k N × 1,5   m   3   m

F y = 1,8   k N

↑ + ∑ F y = 0

R - 4   k N - 6   k N + 1,8   k N = 0  

R = 4   k N + 6   k N - 1,8   k N

R = 8,2   k N

E em seguida, façamos o diagrama de esforço cortante e momento fletor até um pouco depois do ponto R :

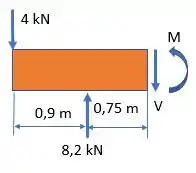
Agora, é só fazer a análise dos esforços cortantes e momento fletor:

↶ + ∑ M = 0

M - 4   k N × 1,65   m   + 8,2   k N × 0,75   m = 0  

M = 4   k N × 1,65   m - 8,2   k N × 0,75   m

M = 450   N ⋅ m

↑ + ∑ F y = 0

8,2   k N - 4   k N - V = 0  

V = 8,2   k N - 4 k N

V = 4,2   k N

Passo 2

Como nossos cálculos anteriores eram comuns aos dois pontos, iremos dividir a questão, resolvendo primeiro o que foi pedido para o ponto A e depois para o ponto B .

Vamos calcular a tensão no ponto A , lembrando que a fórmula do momento polar de inércia de um retângulo é 1 12 ( b h 3 ) onde b é o tamanho da parede paralela ao eixo e h é o tamanho da parede perpendicular ao eixo:

σ A = M y A I

σ A = ( 450   N ⋅ m ) ( 0,1   m ) 1 12 0,2 × 0,2 3 - 0,15 × 0,15 3   m 4

σ A ≅ 0,4937   M P a   ( T r a ç ã o )

E posteriormente, determinamos a tensão máxima de cisalhamento no ponto A pela fórmula abaixo:

τ A = V Q A I t

Como Q A = 0 :

τ A = 0   M P a

Passo 3

Calcularemos, então, as tensões principais no ponto A pela fórmula abaixo:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = 0,4937   M P a + 0   M P a 2 ± 0,4937   M P a - 0   M P a 2 2 + ( 0   M P a ) 2

σ 1,2 = 0,247   M P a ± 0,247   M P a

Onde obtemos duas tensões:

σ 1 ≅ 0,247   M P a + 0,247   M P a

σ 1 ≅ 0,494   M P a

σ 2 ≅ 0,247   M P a - 0,247   M P a

σ 2 ≅ 0   M P a

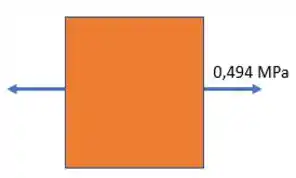
Passo 4

Aqui, repetiremos todos os passos anteriores para o ponto B .

Cálculo da tensão no ponto B :

σ B = M y B I

σ B = ( 450   N ⋅ m ) ( 0,075   m ) 1 12 0,2 × 0,2 3 - 0,15 × 0,15 3   m 4

σ B ≅ - 0,370   M P a   ( C o m p r e s s ã o )

E o cálculo da tensão máxima de cisalhamento no ponto B :

τ B = V Q A I t

Onde, como Q B = 0 :

τ B = 0   M P a

Passo 5

Depois, o cálculo das tensões normais de superfície pela fórmula:

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = ( - 0,370   M P a ) + ( 0   M P a ) 2 ± ( - 0,370   M P a ) - ( 0   M P a ) 2 2 + ( 0   M P a ) 2

σ 1,2 ≅ - 0,185   M P a ± 0,185   M P a

Obtemos novamente, duas tensões:

σ 1 ≅ - 0,185   M P a + 0,185   M P a

σ 1 ≅ 0   M P a

σ 2 ≅ - 0,185   M P a - 0,185   M P a

σ 2 ≅ - 0,370   M P a

Resposta

Tensões principais no ponto A :

σ 1 ≅ 0,494   M P a

σ 2 ≅ 0   M P a

Tensões principais no ponto B :

σ 1 ≅ 0   M P a

σ 2 ≅ - 0,370   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A e no ponto B. Esses
34. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A. Os mancais suportam apenas reações ve
31. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvida em qualquer lugar na superfície do eixo.
30. A viga de abas largas está sujeita às cargas mostradas. Determine a tensão principal na viga no ponto A e no ponto B. Esses pontos estão localizados na parte superior e na parte inferior da alma,
35. O tubo da perfuratriz tem diâmetro externo de 75m m , espessura de parede de 6m m e pesa 0,8k N / m . Se for submetido a um torque e a carga axial como mostra a figura, determine:(a) as tensões pr