Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 131

131- O cilindro tem massa de 36   k g e a barra esbelta uniforme a ele presa tem uma massa m desconhecida. Esse conjunto permanece em equilíbrio estático para valores do ângulo θ de até 45 , mas escorrega se θ exceder 45. Determine m , sabendo-se que o coeficiente de atrito estático vale 0.30 .

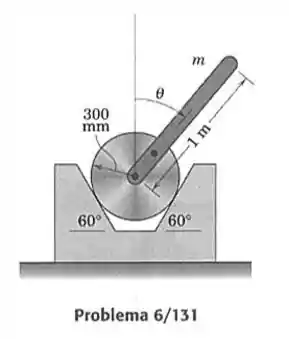
Passo 1

Vamos desenhar o sistema de forças com θ = 45 .

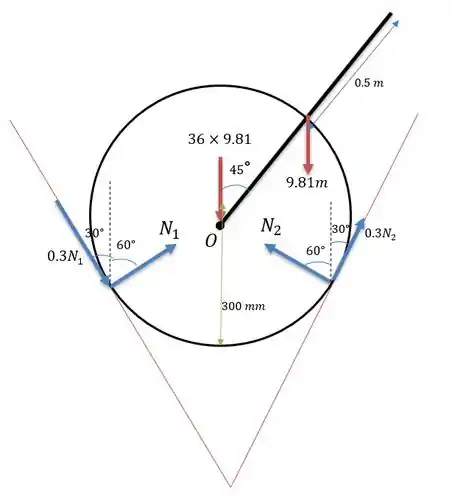
Onde a barra tende a cair, logo o círculo tende a rodar no sentido horário, então o atrito segue a tangente no sentido anti-horário do círculo formado. E não tem como afirmar que N 1 seja igual a N 2 até pela direção das forças de atrito.

Passo 2

Fazendo a somatória das forças verticais no sistema nós temos:

N 1 cos ⁡ 60 + N 2 cos ⁡ 60 - 0.3 N 1 cos ⁡ 30 + 0.3 N 2 cos ⁡ 30 - 36 × 9.81 - 9.81 m = 0

Agora a somatória das forças horizontais nos dá:

N 1 sin ⁡ 60 + 0.3 N 1 sin ⁡ 30 + 0.3 N 2 sin ⁡ 30 - N 2 sin ⁡ 60 = 0

Essa última equação nos dá:

1.016 N 1 - 0.716 N 2 = 0 → N 1 = 0.705 N 2

Agora precisamos calcular a somatória dos momentos em O . Sabendo que as forças normais não geram momento em O e que o raio é perpendicular as forças de atrito nós teremos.

0.3 N 1 + 0.3 N 2 × 0.3 - 9.81 m × 0.5 sin ⁡ 45 = 0

N 1 + N 2 = 38.537 m

Como N 1 = 0.705 N 2 nós encontramos:

1.705 N 2 = 38.537 m → N 2 = 22.602 m

N 1 = 15.934 m

Passo 3

Agora substituindo esses valores de reações normais na equação da somatória de forças verticais nós teremos:

15.934 m cos ⁡ 60 + 22.602 m cos ⁡ 60 - 0.3 cos ⁡ 30 15.934 m

+ 0.3 cos ⁡ 30 22.602 m - 9.81 m = 36 × 9.81

Resolvendo essa equação temos:

11.19 m = 353.16 → m = 31.56   k g

Resposta

m = 31.56   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita Prob. 6/64, somente agora o bloco de concreto de 27 kg começa a se mover para baixo na inclinação de 20 ∘ conforme mostrado. Todas as outras condições permanecem como no Prob. 6/64.
O macaco mostrado foi projetado para levantar carros de carroceria pequena. O parafuso é rosqueado no colar articulado em B e o eixo gira em um rolamento de esferas em A. A rosca tem um diâmetro médio
Para ambas as condições (a) e (b), conforme declarado no Prob. 6/66, determine a magnitude e a direção da força P necessária para começar a abaixar o corpo de 100 lb.
A posição vertical do bloco de 100 kg é ajustada pela cunha ativada por parafuso. Calcule o momento M que deve ser aplicado ao cabo do parafuso para levantar o bloco. O parafuso de rosca única possui
Um disco uniforme de raio r = 250 mm é fixado em A a uma haste AB de 650 mm de massa desprezível que pode girar livremente em um plano vertical em torno de B. se a haste for deslocada 2 ° da posição m