Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 109

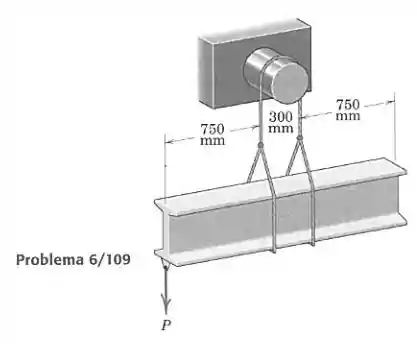
A viga em I uniforme tem uma massa de 74 kg por metro de comprimento e é suportada por uma corda que passa sobre o eixo fixo de 300 mm. Se o coeficiente de atrito entre a corda e o eixo vale 0,5, calcule o menor valor da força P que fará com que a viga saia da sua posição horizontal.

Passo 1

No limiar do tombamento da viga, ela ainda estará em equilíbrio, assim como a corda, e o coeficiente de atrito entre a corda e o eixo é μ = 0,5 . A corda terá trações diferentes T 1 e T 2 em suas extremidades, e a fórmula que relaciona os dois valores para o equilíbrio da corda enrolada no eixo é a seguinte:

ln ⁡ T 2 T 1 = μ β

Sendo T 2 e T 1 as trações maior e menor nas extremidades da corda e β o ângulo total de enrolamento no eixo, no caso igual a π , o ângulo de meia volta. Tendo a relação entre T 1 e T 2 , iremos fazer a equação do equilíbrio da viga, assim determinando P .

Passo 2

Usando a fórmula, vamos encontrar a relação entre T 1 e T 2 . Temos:

ln ⁡ T 2 T 1 = μ β ⇒ ln ⁡ T 1 T 2 = 0,5 π

Passando para a forma exponencial:

T 2 T 1 = e 0,5 π = 4,81

⇒ T 2 = 4,81 T 1

Passo 3

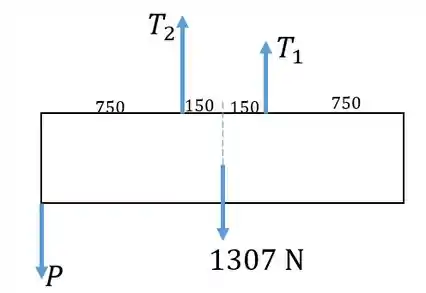
Agora vamos representar a viga em diagrama de corpo livre. Para que a viga não tombe, a tração da corda maior tem que estar na parte da esquerda, para compensar a força P para baixo. A viga possui uma densidade linear de 74 kg por metro, então calculamos o peso W aplicado no meio da viga:

W = m g = 74 × 0,750 + 0,300 + 0,750 × 9,81

= 74 × 1,8 × 9,81

⇒ W = 1307   N

Nosso diagrama de corpo livre então fica assim:

Passo 4

Com as equações de equilíbrio da viga, encontraremos P . Primeiro, fazemos o momento em torno do centro:

∑ M C = 0 ⇒ P 750 + 150 - T 2 150 + T 1 150 = 0

⇒ 900 P - 150 T 2 + 150 T 1 = 0

⇒ 900 P = 150 T 2 - 150 T 1 = 150 ( T 2 - T 1 )

Substituímos T 2 por 4,81 T 1 , como foi determinado no Passo 2:

900 P = 150 4,81 T 1 - T 1 = 150 × 3,81 T 1

⇒ 900 P = 571,5 T 1

Então determinamos T 1 em função de P :

T 1 = 900 571,5 P = 1,575 P

Agora fazemos a soma das forças ser zero:

∑ F = 0 ⇒ - P + T 2 + T 1 - 1307 = 0

Substituímos T 2 por 4,81 T 1 :

- P + 4,81 T 1 + T 1 - 1307 = 0

⇒ - P + 5,81 T 1 - 1307 = 0

Agora substituímos T 1 por 1,575 P :

- P + 5,81 1,575 P - 1307 = 0

⇒ - P + 9,15 P - 1307 = 0

⇒ 8,15 P = 1307

⇒ P = 1307 8,15

⇒ P = 160,3   N

Resposta

P = 160,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mancal de dupla escora está sujeito a uma força axial P = 16k N . Supondo que a escora A suporte 0,75 P e a escora B suporte 0,25 P , ambas com uma distribuição uniforme de pressão, determine o meno
Um disco com diâmetro externo de 120 mm se encaixa livremente em um eixo fixo com diâmetro de 30 mm. Se o coeficiente de atrito estático entre o disco e o eixo é μ s = 0,15 e o disco possui massa de 5
A embreagem de disco é composta de uma placa plana A que desliza sobre o eixo giratório S , o qual é fixado na engrenagem motriz B . Se a engrenagem C , que está entrosada com B , está sujeita a um to
O apoio axial está sujeito a uma distribuição de pressão em sua superfície de contato que varia conforme mostra a figura. Se o coeficiente de atrito estático é μ , determine o torque M necessário para
A luva encaixa-se livremente em torno de um eixo fixo com raio de 50 mm. Se o coeficiente de atrito cinético entre o eixo e a luva é μ k = 0,3 , determine a força P no segmento horizontal da correia d