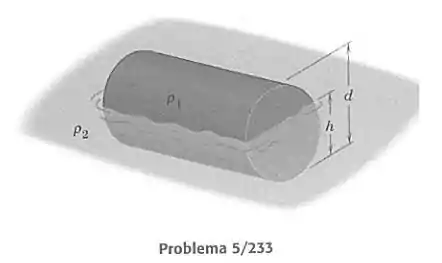
Um cilindro circular de massa específica flutua em um líquido de massa específica . Se é o diâmetro do cilindro e é a altura submersa, faça o gráfico da razão em função de na faixa . Avalie para um cilindro de pinheiro flutuando na água do mar.
Passo 1
Vamos calcular a relação utilizando o princípio da flutuabilidade. Segundo esse princípio, o peso do corpo flutuante deve ser igual ao peso do fluido deslocado por ele, ou seja, igual ao peso de um volume do líquido correspondente ao volume submerso do corpo. O peso do cilindro é:
O peso do líquido deslocado é:
Então:
Onde é o volume total do cilindro e é o volume submerso do corpo. Cortando dos dois lados:
Passo 2
Sabemos que se o cilindro tem comprimento , o volume do cilindro em função de seu diâmetro será:
Como introduzimos esse valor de que não é dado no enunciado, nossa resposta final não pode depender de . Agora devemos calcular o volume submerso em função da profundidade . O volume será a área preenchida pela água na face circular do cilindro vezes :
A área preenchida pela água na face circular é mostrada na figura:
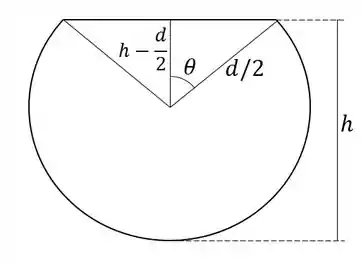
O ângulo da figura varia de 0 a . A área da figura é a área de uma seção de ângulo , mais a área dos dois triângulos. Para calcular a área dos triângulos vamos descobrir o lado que falta:
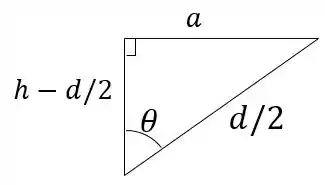
Por Pitágoras:
Então calculamos a área da figura. A área da seção é:
Com em radianos. A área dos triângulos é:
A área total é então:
Perceba que a fórmula funciona também para , quando , pois nesse caso a área da figura é a área da seção menos a área dos triângulos, o que acontece na fórmula pois o valor fica negativo.
Queremos em função apenas de e , então devemos calcular em função desses parâmetros. Temos do triângulo:
Então:
Essa função de fato se adequa ao nosso caso, pois quando e quando . Finalmente, a nossa expressão para é:
Passo 3
Agora voltamos à nossa expressão dada no Passo 1:
Substituímos os valores de e calculados no Passo 2:
Cortamos dos dois lados:
Agora vamos passar para a esquerda e para a direita:
E finalmente, substituindo por :
Passo 4
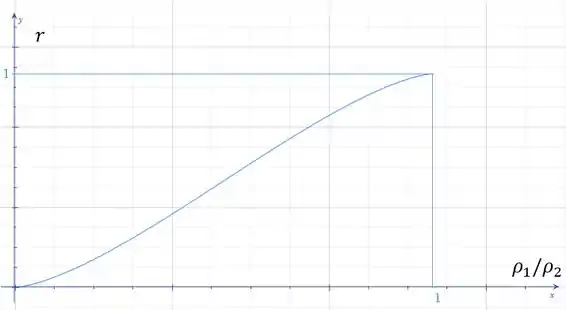
Agora mostramos o gráfico de por :
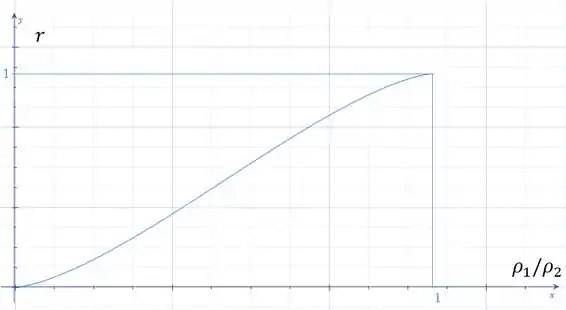
Passo 5
Para o cilindro feito de pinheiro boiando na água do mar, vamos calcular . Temos para o pinheiro uma densidade de e para a água do mar . Então:
Analisando o gráfico obtemos para o valor:
Resposta