Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 133
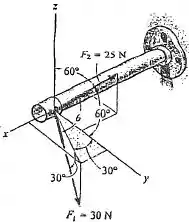
133. Dois cabos exercem forças sobre o tubo. Determine a intensidade da componente projetada de ao longo da linha de ação de .
Passo 1
Primeiro para resolver essa questão temos que achar o vetor unitário que tenha a mesma direção que a força para podermos escrever a força de forma vetorial, para isso vamos usar a fórmula:
Sendo o vetor unitário com a mesma direção de .
Depois que acharmos a força expressa em forma vetorial basta multiplicá-la pelo vetor unitário na direção de , obtendo assim a intensidade da força ao longo da linha de ação de .
Passo 2
Agora para determinar o vetor unitário na direção é fácil já que temos os ângulos de inclinação de .
Para nosso caso temos que a projetar plano para depois achar suas componentes em e e para achar a componente em basta projetá-lo na vertical, então ficamos com:
Logo pode ser obtida com a seguinte operação:
Passo 3
Agora precisamos achar o vetor unitário na direção de , vamos usar o mesmo raciocínio que para o só que com o auxílio da equação do livro, que nos diz o seguinte:
Mais o auxílio da que diz como a achar o vetor unitário com a mesma direção de outro vetor através dos ângulos diretores:
Então para o vetor unitário de temos:
Para achar basta usar a :
Olhando a figura vemos que o ângulo que nos possibilita esse resultado é:
Logo:
Passo 4
Agora só temos que multiplicar por , então:
O fato de ser negativo indica que a projeção dessa força ao longo do eixo de ação de é contraria ao vetor unitário
Resposta
A intensidade de ao longo da linha de ação de é: